
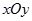 中,已知圆
中,已知圆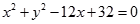 的圆心为
的圆心为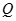 ,过点
,过点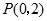 且斜率为
且斜率为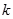 的直线与圆
的直线与圆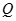 相交于不同的两点
相交于不同的两点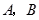 .
.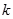 的取值范围;
的取值范围;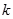 ,使得直线OD与PQ平行?如果存在,求
,使得直线OD与PQ平行?如果存在,求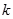 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.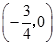 ;(Ⅱ)没有符合题意的常数
;(Ⅱ)没有符合题意的常数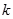 ,理由见解析.
,理由见解析.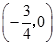 ;(Ⅱ)由向量加减法,可利用向量处理,设
;(Ⅱ)由向量加减法,可利用向量处理,设 ,则
,则 ,由
,由 与
与 共线等价于
共线等价于 ,然后由根与系数关系可得
,然后由根与系数关系可得 ,由(Ⅰ)知
,由(Ⅰ)知 ,故没有符合题意的常数
,故没有符合题意的常数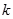 .注意运用向量法和方程的思想.
.注意运用向量法和方程的思想. ,所以圆心为
,所以圆心为 ,
,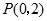 且斜率为
且斜率为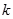 的直线方程为
的直线方程为 .
. ,整理得
,整理得 . ①
. ①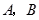 等价于
等价于 ,
, ,即
,即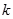 的取值范围为
的取值范围为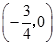 .
. ,则
,则 ,
, ②
② . ③
. ③ .
. 与
与 共线等价于
共线等价于 ,
,
 ,故没有符合题意的常数
,故没有符合题意的常数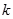 .
.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源:不详 题型:解答题
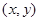 到定点
到定点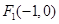 与到定点
与到定点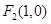 的距离之比为3.
的距离之比为3.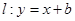 ,若曲线C上恰有两个点到直线
,若曲线C上恰有两个点到直线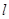 的距离为1,
的距离为1,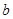 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
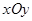 中,圆
中,圆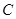 的参数方程为
的参数方程为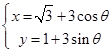 (
(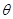 为参数),以
为参数),以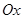 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线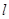 的极坐标方程为
的极坐标方程为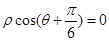 .
.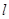 的直角坐标方程和圆
的直角坐标方程和圆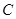 的普通方程;
的普通方程;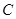 截直线
截直线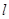 所得的弦长.
所得的弦长.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
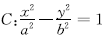 的左、右焦点分别为F1、F2,点P在右支上,且PF1与圆x2+y2=a2相切,切点为PF1的中点,F2到一条渐近线的距离为3,则
的左、右焦点分别为F1、F2,点P在右支上,且PF1与圆x2+y2=a2相切,切点为PF1的中点,F2到一条渐近线的距离为3,则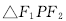 的面积为 ( )
的面积为 ( )| A.9 | B.3 | C.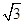 | D.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com