
【题目】湖北省第二届(荆州)园林博览会于2019年9月28日至11月28日在荆州园博园举办,本届园林博览会以“辉煌荆楚,生态园博”为主题,展示荆州生态之美,文化之韵,吸引更多优秀企业来荆投资,从而促进荆州经济快速发展.在此博览会期间,某公司带来了一种智能设备供采购商洽谈采购,并决定大量投放荆州市场.已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备![]() 万台,且全部售完,且每万台的销售收入
万台,且全部售完,且每万台的销售收入![]() (万元)与年产量
(万元)与年产量![]() (万台)的函数关系式近似满足
(万台)的函数关系式近似满足
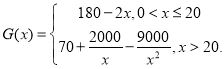
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万台)的函数解析式.(年利润
(万台)的函数解析式.(年利润![]() 年销售收入
年销售收入![]() 总成本).
总成本).
(2)当年产量为多少万台时,该公司获得的利润最大?并求最大利润.
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①在线性回归模型中,相关指数![]() 越接近于1,表示回归效果越好;
越接近于1,表示回归效果越好;
②两个变量相关性越强,则相关系数r就越接近于1;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位;
平均减少0.5个单位;
④两个模型中残差平方和越小的模型拟合的效果越好.
⑤回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
⑥若![]() 的观测值满足
的观测值满足![]() ≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
⑦从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误. 其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于![]() 的偶数可以表示为两个素数的和”,如
的偶数可以表示为两个素数的和”,如![]() .现从不超过
.现从不超过![]() 的素数中,随机选取两个不同的数(两个数无序).(注:不超过
的素数中,随机选取两个不同的数(两个数无序).(注:不超过![]() 的素数有
的素数有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(1)列举出满足条件的所有基本事件;
(2)求“选取的两个数之和等于![]() ”事件发生的概率.
”事件发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某社区80个人,以研究这一社区居民在晚上8点至十点时间段的休闲方式与性别的关系,得到下面的数据表:

(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,求这3人中至少有1人是以看书为休闲方式的概率;
(2)根据以上数据,能否有99%的把握认为“在晚上8点至十点时间段的休闲方式与性别有关系?”
参考公式: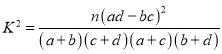 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆锥的高,
是圆锥的高,![]() 是圆锥底面的直径,
是圆锥底面的直径,![]() 是底面圆周上一点,
是底面圆周上一点,![]() 是
是![]() 的中点,平面
的中点,平面![]() 和平面
和平面![]() 将圆锥截去部分后的几何体如图所示.
将圆锥截去部分后的几何体如图所示.
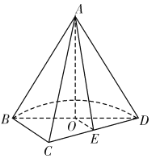
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com