
【题目】如图,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() .
.
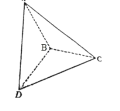
(Ⅰ)求证:![]() ;
;
(Ⅱ)求直线AB与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据题意,过点A作![]() ,垂足为O,连接OD,证明
,垂足为O,连接OD,证明![]() ,根据线面垂直的判定定理,证明
,根据线面垂直的判定定理,证明![]() 平面AOD,再根据线面垂直的性质定理证明
平面AOD,再根据线面垂直的性质定理证明![]() 。
。
(Ⅱ)设点B在平面ADC上的投影为点H,则![]() 就是直线AB与平面ADC所成角.法一找直角三角形,利用勾股定理求得
就是直线AB与平面ADC所成角.法一找直角三角形,利用勾股定理求得![]() ,从而求出
,从而求出![]() ,法二利用等体积法求出
,法二利用等体积法求出![]() ,从而求得;法三建立坐标系,利用向量法,求出平面
,从而求得;法三建立坐标系,利用向量法,求出平面![]() 的法向量,再根据利用向量法求夹角余弦值求得。
的法向量,再根据利用向量法求夹角余弦值求得。
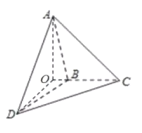
(Ⅰ)证明:过点A作![]() ,垂足为O,连接OD.
,垂足为O,连接OD.
由![]() ,得
,得![]() ,
,
而![]() ,
,![]() ,则
,则![]() 与
与![]() 全等,
全等,
故![]() ,即
,即![]() ,
,
而![]() ,故
,故![]() 平面AOD ,
平面AOD ,
而![]() 平面AOD,故
平面AOD,故![]() ;
;
(Ⅱ)解法1:设点B在平面ADC上的投影为点H,
则![]() 就是直线AB与平面ADC所成角.
就是直线AB与平面ADC所成角.
由AB=BC=BD,可知HA=HC=HD,点H为△ADC的外心
由(Ⅰ)知,![]() 就是直二面角
就是直二面角![]() 的平面角,故
的平面角,故![]() .
.
设![]() ,利用勾股定理等知识,求得
,利用勾股定理等知识,求得![]() ,
,
因此,![]() ,
,
故直线AB与平面ADC所成角的余弦值为![]() .
.
解法2:设点B在平面ADC上的投影为点H,
则∠BAH就是直线AB与平面ADC所成角.
由(Ⅰ)知,![]() 就是直二面角
就是直二面角![]() 的平面角,故
的平面角,故![]() ,
,
设![]() ,利用
,利用![]() ,求得
,求得![]() ,
,
因此,![]() ,
,![]() .
.
故直线AB与平面ADC所成角的余弦值为![]() .
.
解法3:
由(Ⅰ)知,![]() 就是直二面角
就是直二面角![]() 的平面角,故
的平面角,故![]() ,
,
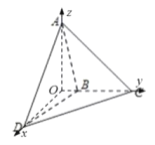
建立如图的空间直角坐标系Oxyz,设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
于是,![]() ,
,![]() ,
,![]() ,
,
设平面ADC的法向量为![]() ,则
,则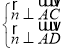 ,即
,即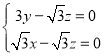 .
.
解得![]() ,
,
设所求线面角为![]() ,则
,则![]() ,
,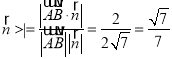 ,
,
因此,![]() ,故直线AB与平面ADC所成角的余弦值为
,故直线AB与平面ADC所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 为等比数列,
为等比数列,![]() 公比为
公比为![]()
![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)若![]() 求
求![]()
(2)若调换![]() 的顺序后能构成一个等差数列,求
的顺序后能构成一个等差数列,求![]() 的所有可能值;
的所有可能值;
(3)是否存在正常数![]() 使得对任意正整数
使得对任意正整数![]() 不等式
不等式![]() 总成立?若存在,求出
总成立?若存在,求出![]() 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 函数
函数![]()
(1)当![]() 时,解不等式
时,解不等式![]()
(2)若关于![]() 的方程
的方程![]() 的解集中怡好有一个元素,求
的解集中怡好有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() 若对任意
若对任意![]() 函数
函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖北省第二届(荆州)园林博览会于2019年9月28日至11月28日在荆州园博园举办,本届园林博览会以“辉煌荆楚,生态园博”为主题,展示荆州生态之美,文化之韵,吸引更多优秀企业来荆投资,从而促进荆州经济快速发展.在此博览会期间,某公司带来了一种智能设备供采购商洽谈采购,并决定大量投放荆州市场.已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备![]() 万台,且全部售完,且每万台的销售收入
万台,且全部售完,且每万台的销售收入![]() (万元)与年产量
(万元)与年产量![]() (万台)的函数关系式近似满足
(万台)的函数关系式近似满足
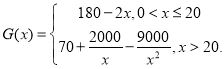
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万台)的函数解析式.(年利润
(万台)的函数解析式.(年利润![]() 年销售收入
年销售收入![]() 总成本).
总成本).
(2)当年产量为多少万台时,该公司获得的利润最大?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com