解:(1)∵函数是奇函数,
∴f(1)+f(-1)=0,可得
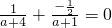
,解之得a=2-----------(3分)
检验:a=2时,
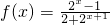
,
∴
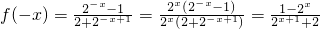
∴f(x)+f(-x)=0对x∈R恒成立,即f(x)是奇函数.-----------(5分)
(2)证明:令t=2
x,则
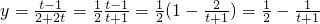
设x
1∈R,x
2∈R且x
1<x
2
∵t=2
x在R上是增函数,∴0<t
1<t
2当0<t
1<t
2时,
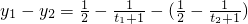
=
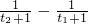
=

∵0<t
1<t
2
∴t
1-t
2<0,t
1+1>0,t
2+1>0
∴y
1<y
2,可得f(x)在R上是增函数---------------(10分)
(3)∵f(x)是奇函数
∴不等式f(mt
2+1)+f(1-mt)>0等价于f(mt
2+1)>f(mt-1)
∵f(x)在R上是增函数
∴对任意的t∈R,不原不等式恒成立,即mt
2+1>mt-1对任意的t∈R恒成立,
化简整理得:mt
2-mt+2>0对任意的t∈R恒成立
1°m=0时,不等式即为2>0恒成立,符合题意;
2°m≠0时,有
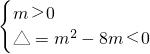
即0<m<8
综上所述,可得实数m的取值范围为0≤m<8-------------(16分)
分析:(1)根据奇函数的定义,取x=1,得f(1)+f(-1)=0,解之得a=2,再经过检验可得当a=2时,f(x)+f(-x)=0对x∈R恒成立,所以f(x)是奇函数;
(2)令t=2
x,得
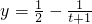
,再用单调性的定义,证出当x
1∈R,x
2∈R且x
1<x
2时,y
1-y
2=

,讨论可得y
1<y
2,所以f(x)在R上是增函数;
(3)因为f(x)是奇函数,并且在R上是增函数,所以原不等式对任意的t∈R恒成立,即mt
2+1>mt-1对任意的t∈R恒成立,化简整理得关于t的一元二次不等式,最后经过分类讨论,可得实数m的取值范围为0≤m<8.
点评:本题以含有指数式的分式函数为例,考查了函数的单调性与奇偶性等简单性质和一元二次不等式恒成立等知识点,属于中档题.

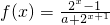 是奇函数.
是奇函数.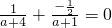 ,解之得a=2-----------(3分)
,解之得a=2-----------(3分)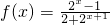 ,
,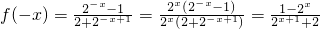
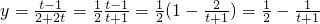
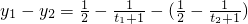 =
=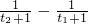 =
=
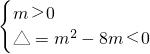 即0<m<8
即0<m<8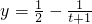 ,再用单调性的定义,证出当x1∈R,x2∈R且x1<x2时,y1-y2=
,再用单调性的定义,证出当x1∈R,x2∈R且x1<x2时,y1-y2= ,讨论可得y1<y2,所以f(x)在R上是增函数;
,讨论可得y1<y2,所以f(x)在R上是增函数;
