
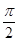 ”的______条件.
”的______条件.科目:高中数学 来源:不详 题型:解答题
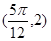 在函数
在函数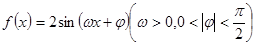 的图象上,直线
的图象上,直线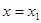 、
、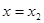 是
是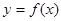 图象的任意两条对称轴,且
图象的任意两条对称轴,且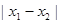 的最小值为
的最小值为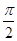 .
.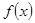 的单递增区间和其图象的对称中心坐标;
的单递增区间和其图象的对称中心坐标;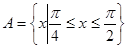 ,
,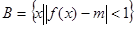 ,若
,若 ,求实数
,求实数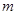 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
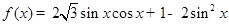 ,xÎR.
,xÎR.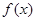 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;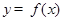 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的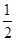 ,把所得到的图象再向左平移
,把所得到的图象再向左平移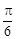 单位,得到函数
单位,得到函数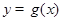 的图象,求函数
的图象,求函数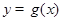 在区间
在区间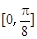 上的最小值.
上的最小值. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 时,f(x)的最大值为2.
时,f(x)的最大值为2. ,
, ]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.
]上是否存在f(x)的对称轴?如果存在求出其对称轴.若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
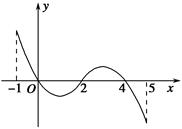
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的单调递增区间是
的单调递增区间是 (k∈Z);
(k∈Z);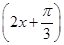 的定义域是
的定义域是 ;
; 上的最大值为
上的最大值为 +1,最小值为0.
+1,最小值为0.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
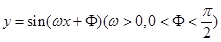 一个周期内的图象上的四个点,如图所示,
一个周期内的图象上的四个点,如图所示,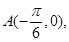 B为
B为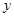 轴上的点,C为图像上的最低点,E为该函数图像的一个对称中心,B与D关于点E对称,
轴上的点,C为图像上的最低点,E为该函数图像的一个对称中心,B与D关于点E对称,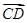 在
在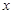 轴上的投影为
轴上的投影为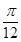 ,则
,则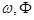 的值为( )
的值为( )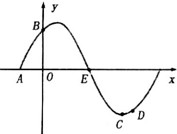
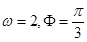 B.
B.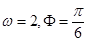
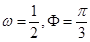 D.
D.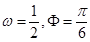
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
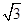 cos2ωx-
cos2ωx-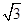 (其中ω>0),且函数f(x)的周期为π.
(其中ω>0),且函数f(x)的周期为π.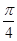 个单位长度,再将所得图象各点的横坐标缩小到原来的
个单位长度,再将所得图象各点的横坐标缩小到原来的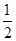 倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在
倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在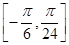 上的单调区间.
上的单调区间.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com