练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知命题p：“∀x∈[1,2]，x2－a≥0”，命题q：“∃x0∈R，x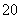＋2ax0＋2－a＝0”，若命题“p且q”是真命题，求实数a的取值范围．


    ∵“p且q”是真命题，

    ∴p为真命题，q也为真命题．

    若p为真命题，∵x∈[1,2]时，a≤x2恒成立，

    ∴a≤1.

    若q为真命题，即x2＋2ax＋2－a＝0有实根，Δ＝4a2－4(2－a)≥0，

    ∴a≥1或a≤－2，

    综上知所求实数a的取值范围是a≤－2或a＝1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数若有则的取值范围为（　　）

    A．    B．  C．    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知R为全集，A＝{x|(1－x)·(x＋2)≤0}，则∁RA＝(　　)

    A．{x|x<－2，或x>1}                                   B．{x|x≤－2，或x≥1}

    C．{x|－2<x<1}                                             D．{x|－2≤x≤1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合A＝{x|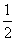<2x<2}，B＝{x|lgx>－1}，则A∪B＝(　　)

    A．{x|x>－1}                                                B．{x|－1<x<1}

    C．{x|x>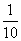}                                                D．{x|－1<x<10或x>10}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题p：∃m∈R，m＋1≤0，命题q：∀x∈R，x2＋mx＋1>0恒成立．若p∨q为假命题，则实数m的取值范围是(　　)

    A．m≥2                                                       B．m≤－2

    C．m≤－2或m≥2                                       D．－2≤m≤2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列结论：

    ①若命题p：∃x∈R，tanx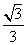＝；命题q：∀x∈R，x2－x＋1>0.则命题“p∧(綈q)”是假命题；

    ②已知直线l1：ax＋3y－1＝0，l2：x＋by＋1＝0，则l1⊥l2的充要条件是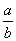＝－3；

    ③命题“若x2－3x＋2＝0，则x＝1”的逆否命题为：“若x≠1，则x2－3x＋2≠0”．其中正确结论的序号为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    方程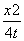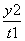＋＝1表示曲线C，给出以下命题：

    ①曲线C不可能为圆；

    ②若1<t<4，则曲线C为椭圆；

    ③若曲线C为双曲线，则t<1或t>4；

    ④若曲线C为焦点在x轴上的椭圆，则1<t<.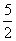

    其中真命题的序号是______(写出所有正确命题的序号)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设角α，β是锐角，则“α＋β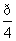＝”是“(1＋tanα)(1＋tanβ)＝2”的(　　)

    A．充分不必要条件                                      B．必要不充分条件

    C．充要条件                                                 D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝则f(f(3))＝(　　)

    A.                                                              B．3

    C.                                                             D.

    查看答案和解析>>

    同步练习册答案