
ЗжЮі ЃЈЂёЃЉИљОнЦНУцЯђСПЕФЪ§СПЛ§гыФЃГЄЙЋЪНЃЌЯШЧѓГі$\overrightarrow{a}$•$\overrightarrow{b}$ЕФжЕЃЌдйЧѓГі|$\overrightarrow{a}$-$\overrightarrow{b}$|ЃЛ
ЃЈЂђЃЉИљОнЦНУцЯђСПЕФЪ§СПЛ§гыМаНЧЙЋЪНЃЌМДПЩЧѓГі$\overrightarrow{m}$ЁЂ$\overrightarrow{n}$МаНЧЕФгрЯвжЕЃЎ
НтД№ НтЃКЃЈЂёЃЉ$\overrightarrow{a}$ЃЌ$\overrightarrow{b}$ЪЧСНИіЕЅЮЛЯђСПЃЌ
ЕБ|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2ЪБЃЌ${ЃЈ\overrightarrow{a}-2\overrightarrow{b}ЃЉ}^{2}$=${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$=1-4$\overrightarrow{a}$•$\overrightarrow{b}$+4=4ЃЌ
Ёр$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{4}$ЃЌ
Ёр${ЃЈ\overrightarrow{a}-\overrightarrow{b}ЃЉ}^{2}$=${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=1-2ЁС$\frac{1}{4}$+1=$\frac{3}{2}$ЃЌ
Ёр|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$ЃЛ
ЃЈЂђЃЉШє$\overrightarrow{a}$ЃЌ$\overrightarrow{b}$ЕФМаНЧЮЊ60ЁуЃЌдђ$\overrightarrow{a}$•$\overrightarrow{b}$=1ЁС1ЁСcos60Ёу=$\frac{1}{2}$ЃЌ
гжЯђСП$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$ЃЌ$\overrightarrow{n}$=$\overrightarrow{a}$-3$\overrightarrow{b}$ЃЌ
Ёр$\overrightarrow{m}$•$\overrightarrow{n}$=${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}$•$\overrightarrow{b}$-3${\overrightarrow{b}}^{2}$=1-2ЁС$\frac{1}{2}$-3ЁС1=-3ЃЌ
|$\overrightarrow{m}$|=$\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{1+2ЁС\frac{1}{2}+1}$=$\sqrt{3}$ЃЌ
|$\overrightarrow{n}$|=$\sqrt{{\overrightarrow{a}}^{2}-6\overrightarrow{a}•\overrightarrow{b}+{9\overrightarrow{b}}^{2}}$=$\sqrt{1-6ЁС\frac{1}{2}+9}$=$\sqrt{7}$ЃЌ
Ёр$\overrightarrow{m}$ЁЂ$\overrightarrow{n}$ЕФМаНЧІШЕФгрЯвжЕЮЊ
cosІШ=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|ЁС|\overrightarrow{n}|}$=$\frac{-3}{\sqrt{3}ЁС\sqrt{7}}$=-$\frac{\sqrt{21}}{7}$ЃЎ
ЕуЦР БОЬтПМВщСЫЦНУцЯђСПЕФЪ§СПЛ§гыФЃГЄЙЋЪНвдМАМаНЧЙЋЪНЕФгІгУЮЪЬтЃЌЪЧЛљДЁЬтФПЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 11110 | BЃЎ | 10101 | CЃЎ | 10011 | DЃЎ | 10001 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 1 | BЃЎ | 2 | CЃЎ | $\frac{{2\sqrt{3}}}{3}$ | DЃЎ | $\sqrt{3}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 1 | BЃЎ | 2 | CЃЎ | 3 | DЃЎ | 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 5 | BЃЎ | {5} | CЃЎ | ∅ | DЃЎ | {1ЃЌ2ЃЌ3ЃЌ4} |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | gЃЈxЃЉ=x2 | BЃЎ | $gЃЈxЃЉ=\frac{1}{x}$ | CЃЎ | gЃЈxЃЉ=x3 | DЃЎ | $gЃЈxЃЉ={x^{\frac{1}{2}}}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
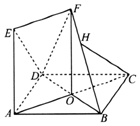 ШчЭМЃЌе§ЗНаЮABCDЕФЖдНЧЯпACгыBDЯрНЛгкЕуOЃЌЫФБпаЮOAEFЮЊОиаЮЃЌЦНУцOAEFЁЭЦНУцABCDЃЌAB=AEЃЎ
ШчЭМЃЌе§ЗНаЮABCDЕФЖдНЧЯпACгыBDЯрНЛгкЕуOЃЌЫФБпаЮOAEFЮЊОиаЮЃЌЦНУцOAEFЁЭЦНУцABCDЃЌAB=AEЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ВЛДцдкx0ЁЪRЃЌ$x_0^2+{x_0}+1Ён0$ | BЃЎ | ?x0ЁЪRЃЌ$x_0^2+{x_0}+1Ён0$ | ||
| CЃЎ | ?xЁЪRЃЌx2+x+1ЃМ0 | DЃЎ | ?xЁЪRЃЌx2+x+1Ён0 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com