
| A. | a>0且b=0 | B. | a>0且b>0 | C. | a=0且b>0 | D. | a<0且b=0 |
分析 题中原方程g2(x)-ag(x)+b=0有且只有7个不同实数解,结合函数图象,对g(x)的取值情况进行分析,进而得出答案.
解答 解:g(x)图象如图: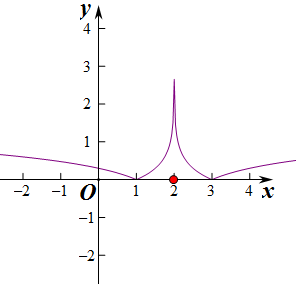
令g(x)=t,
由图象可得:g(x)=t>0有4个不相等的根,g(x)=t=0有3个不相等的根,g(x)=t<0没有实数根.
∵题中原方程g2(x)-ag(x)+b=0有且只有7个不同实数解,
∴t2-at+b=0有两个实根,且一根为0,一根大于零
∴a>0,b=0,
故选A.
点评 数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 70 | C. | 110 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π | B. | 是奇函数 | ||
| C. | 在区间$(-\frac{1}{12}π,\frac{5}{12}π)$上单调递减 | D. | $(\frac{5}{12}π,0)$为其图象的一个对称中心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com