
如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.
科目:高中数学 来源: 题型:填空题
对于具有相同定义域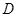 的函数
的函数 和
和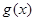 ,若存在
,若存在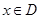 ,使得
,使得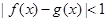 ,则
,则 和
和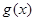 在
在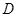 上是“亲密函数”.给出定义域均为
上是“亲密函数”.给出定义域均为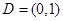 的四组函数如下:
的四组函数如下:
①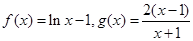 ②
②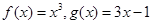
③ 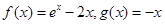 ④
④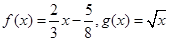
其中,函数 和
和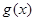 在
在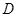 上是“亲密函数”的是 .
上是“亲密函数”的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com