
分析 (1)由已知可得关于a,b,c的方程组,求解方程组得到a,b的值,则椭圆方程可求.
(2)设直线AC的方程,代入椭圆方程,利用韦达定理以及弦长公式即可求得|AC|的值,将$-\frac{1}{k}$代入上式可得|BD|,由k2>0,即可求得$\frac{|AC|}{|BD|}$的取值范围.
解答 解:(1)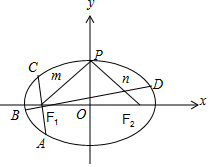 如图,设|PF1|=m,|PF2|=n,由$\frac{sin∠P{F}_{1}{F}_{2}+sin∠P{F}_{2}{F}_{1}}{sin∠{F}_{1}P{F}_{2}}$=2,
如图,设|PF1|=m,|PF2|=n,由$\frac{sin∠P{F}_{1}{F}_{2}+sin∠P{F}_{2}{F}_{1}}{sin∠{F}_{1}P{F}_{2}}$=2,
得$\frac{m+n}{2c}=2$,即$\frac{2a}{2c}=\frac{a}{c}=1$,
由△PF1F2的面积的最大值为$\sqrt{3}$,得bc=$\sqrt{3}$.
联立$\left\{\begin{array}{l}{a=c}\\{bc=\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=$\sqrt{3}$.
∴椭圆E的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)当直线AC斜率不存在时,$\frac{|AC|}{|BD|}$=$\frac{3}{4}$,当直线AC斜率为0时,$\frac{|AC|}{|BD|}$=$\frac{4}{3}$,
当直线AC斜率存在且不为0时,设直线AC:y=k(x+1),A(x1,y1)C(x2,y2),BD:$y=-\frac{1}{k}(x+1)$,
联立$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得(3+4k2)x2+8k2x+4k2-12=0,
∴${x}_{1}+{x}_{2}=-\frac{8{k}^{2}}{3+4{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
则|AC|=$\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$.
将$-\frac{1}{k}$代入上式可得|BD|=$\frac{12(1+{k}^{2})}{4+3{k}^{2}}$,
则$\frac{|AC|}{|BD|}$=$\frac{3{k}^{2}+4}{4{k}^{2}+3}=\frac{3}{4}+\frac{7}{4}•\frac{1}{4{k}^{2}+3}$,
由k2>0,则$\frac{3}{4}<\frac{3}{4}+\frac{7}{4}•\frac{1}{4{k}^{2}+3}<\frac{4}{3}$,
综上,$\frac{|AC|}{|BD|}$的取值范围为[$\frac{3}{4}$,$\frac{4}{3}$].
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,考查计算能力,是中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2-ln4}{4}$ | B. | $\frac{3-2ln4}{4}$ | C. | $\frac{1+ln4}{4}$ | D. | $\frac{1+2ln4}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p为真,则¬(¬p)也为真 | |
| B. | 若“p∧q为真”,则“p∨q为真”为真命题 | |
| C. | ?x∈R,使得tanx=2017 | |
| D. | “2x>$\frac{1}{2}$”是“log${\;}_{\frac{1}{2}}$x<0”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | log23 | C. | 3 | D. | -log25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{2}}]∪({\frac{{3\sqrt{3}}}{8},\frac{3}{2}}]$ | C. | $({-∞,-\frac{3}{2}})∪({\frac{{3\sqrt{3}}}{8},\frac{3}{2}})$ | D. | $[{-\frac{3}{2},+∞})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com