
分析 (1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=$\sqrt{2}$sin($\frac{x}{2}$+45°),由周期公式即可得解.
(2)由x∈[-90°,90°]解得$\frac{x}{2}$+45°的范围,可求sin($\frac{x}{2}$+45°)的范围,即可求得函数f(x)的最值.
(3)由x∈[0°,180°),可求$\frac{x}{2}$+45°的范围,根据正弦函数的图象和性质即可求的f(x)在[0,180)上的减区间.
解答 解:(1)∵f(x)=cos(-$\frac{x}{2}$)+sin($π-\frac{x}{2}$)=cos($\frac{x}{2}$)+sin($\frac{x}{2}$)=$\sqrt{2}$sin($\frac{x}{2}$+45°),
∴函数f(x)的最小正周期T=$\frac{2π}{\frac{1}{2}}$=4π.
(2)∵x∈[-90°,90°],
∴$\frac{x}{2}$∈[-45°,45°],$\frac{x}{2}$+45°∈[0,90°],
∴sin($\frac{x}{2}$+45°)∈[0,1],
∴函数f(x)=$\sqrt{2}$sin($\frac{x}{2}$+45°)的最大值为$\sqrt{2}$,最小值为0.
(3)∵x∈[0°,180°),
∴$\frac{x}{2}$∈[0,90°),$\frac{x}{2}$+45°∈[45°,135°),
∴f(x)=$\sqrt{2}$sin($\frac{x}{2}$+45°)在[0,180)上的减区间为:[90°,180°).
点评 本题主要考查了三角函数中的恒等变换应用,余弦函数的图象和性质,属于基本知识的考查.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
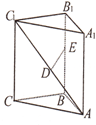 如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点
如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com