
分析 (Ⅰ)由椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(常数a>1)的离心率为$\frac{\sqrt{2}}{2}$,求出a,由此能求出椭圆C的方程.
(Ⅱ)设M(x1,y1),N(x2,y2)是椭圆γ上的两个动点,由条件得:$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,x1x2+y1y2=-2+1=-1,由此能求出|MN|.
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(常数a>1)的离心率为$\frac{\sqrt{2}}{2}$,
∴$\frac{\sqrt{{a}^{2}-1}}{a}$=$\frac{\sqrt{2}}{2}$,解得a=$\sqrt{2}$,
∴椭圆C的方程是$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(Ⅱ)∵M、N是椭圆C上的两个不同动点,O为坐标原点,
A(a,1),B(-a,1),满足kOM•kON=kOA•kOB,
∴A($\sqrt{2}$,1),B(-$\sqrt{2}$,1),
设M(x1,y1),N(x2,y2)是椭圆γ上的两个动点,满足kOM•kON=kOA•kOB,
由条件得:$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,x1x2+y1y2=$\frac{1}{2}{x}_{1}{x}_{2}$.
平方得:x12x22=4y12y22=(2-x12)(2-x22),即x12+x22=2-x12x22,
∴${{y}_{1}}^{2}+{{y}_{2}}^{2}$=2-$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{2}$=1+$\frac{{{x}_{1}}^{2}{{x}_{2}}^{2}}{2}$,
∴|MN|=$\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}$=$\sqrt{{{x}_{2}}^{2}+{{x}_{1}}^{2}-2{x}_{1}{x}_{2}+{{y}_{1}}^{2}+{{y}_{2}}^{2}-2{y}_{1}{y}_{2}}$
=$\sqrt{3-2({x}_{1}{x}_{2}+{y}_{1}{y}_{2})-\frac{1}{2}{{x}_{1}}^{2}{{x}_{2}}^{2}}$
=$\sqrt{3-{x}_{1}{x}_{2}-\frac{1}{2}{{x}_{1}}^{2}{{x}_{2}}^{2}}$
=$\sqrt{-\frac{1}{2}({x}_{1}{x}_{2}+1)^{2}+\frac{5}{2}}$.
∴|MN|取值范围是[$\sqrt{2}$,2].
点评 此题考查了椭圆的简单性质,二次函数的性质,斜率公式,以及平面向量的数量积运算,熟练掌握运算法则是解本题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 3 | C. | 6 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 500人 | x人 | z人 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
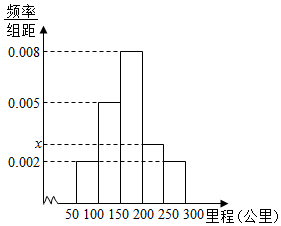 2015年1月1日新《环境保护法》实施后,2015年3月18日,交通运输部发布《关于加快推进新能源汽车在交通运输行业推广应用的实施意见》,意见指出,至2020年,新能源汽车在交通运输行业的应用初具规模,在城市公交、出租汽车和城市物流配送等领域的总量达到30万辆;新能源汽车配套服务设施基本完备,新能源汽车运营效率和安全水平明显提升.随着新能源汽车的迅速发展,关于新能源汽车是纯电动汽车的续航里程(单次充电后能行驶的最大里程)一直是消费者最为关注的话题.
2015年1月1日新《环境保护法》实施后,2015年3月18日,交通运输部发布《关于加快推进新能源汽车在交通运输行业推广应用的实施意见》,意见指出,至2020年,新能源汽车在交通运输行业的应用初具规模,在城市公交、出租汽车和城市物流配送等领域的总量达到30万辆;新能源汽车配套服务设施基本完备,新能源汽车运营效率和安全水平明显提升.随着新能源汽车的迅速发展,关于新能源汽车是纯电动汽车的续航里程(单次充电后能行驶的最大里程)一直是消费者最为关注的话题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com