练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．设函数f（x）满足f（x）=2f（$\frac{1}{x}$）•x-1，则f（4）的值是（　　）
    A．3B．-3C．-1D．1

    分析 因为括号里一个是x，一个是$\frac{1}{x}$，互为倒数 又求的是f（4），所以想到分别把x用4跟$\frac{1}{4}$替换，联立两式能求出f（4）．

    解答 解：∵函数f（x）满足f（x）=2f（$\frac{1}{x}$）•x-1，
    ∴$\left\{\begin{array}{l}{f（4）=2f（\frac{1}{4}）×4-1}\\{f（\frac{1}{4}）=2f（4）×\frac{1}{4}-1}\end{array}\right.$，
    解得f（4）=3，f（$\frac{1}{4}$）=$\frac{1}{2}$．
    故选：A．

    点评 本题考查函数值的求法，是中档题，解题时要认真审题，注意函数性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．f（x）=x2+x+1，则f（f（2））=57．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．若角α的终边落在直线y=-3x上，求sinα，cosα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

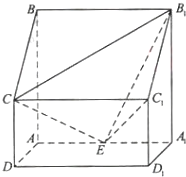    14．如图，四棱柱ABCD-A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD=CD=1，AA1=AB=2，E为棱AA1的中点．
    （1）证明B1C1⊥CE；
    （2）（理）求二面角B1-CE-C1的正弦值．
    （文）求异面直线CE与AD所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

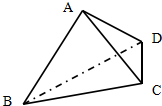    1．如图：已知空间四边形ABCD中，AB=BC=CD=DA=a，对角线AC=$\frac{{\sqrt{6}}}{2}a$，BD=$\sqrt{2}a$，求二面角A-BD-C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．一个等差数列{an}的前n项和为12，前2n项和为24，则前3n项和为（　　）
    A．36B．48C．38D．40

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知f（x）=$\frac{1}{x}$，则$\underset{lim}{△x→0}$$\frac{f（x-2△x）-f（x）}{△x}$的值是（　　）
    A．$\frac{2}{x^2}$B．2xC．-2xD．-$\frac{2}{x^2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知函数y=f（x）是奇函数，且当x＞0时，f（x）=2x+1，则f（-2）=（　　）
    A．-3B．3C．5D．-5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．函数f（x）=ax2+bx+c，已知方程f（x）=x无实数解．
    求证：f（f（x））=x也没有实数解．

    查看答案和解析>>

    同步练习册答案