
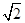 ]上的最小值.
]上的最小值.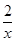 .(2)函数f(x)+g(x)是奇函数.
.(2)函数f(x)+g(x)是奇函数.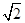 ]上的最小值是2
]上的最小值是2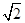 .
.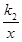 ,其中k1k2≠0然后结合已知中点的坐标的,饿到结论。
,其中k1k2≠0然后结合已知中点的坐标的,饿到结论。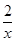 ,
,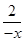 =-(x+
=-(x+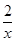 )=-h(x)得到证明。
)=-h(x)得到证明。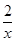 ,设x1,x2是(0,
,设x1,x2是(0,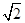 ]上的任意两个实数,且x1<x2,,然后运用定义法得到单调性,确定最值。
]上的任意两个实数,且x1<x2,,然后运用定义法得到单调性,确定最值。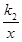 ,其中k1k2≠0.
,其中k1k2≠0.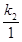 =2.
=2.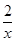 .
.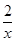 ,
,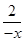 =-(x+
=-(x+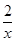 )=-h(x),
)=-h(x),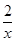 ,设x1,x2是(0,
,设x1,x2是(0,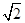 ]上的任意两个实数,且x1<x2,
]上的任意两个实数,且x1<x2,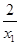 )-(x2+
)-(x2+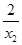 )=(x1-x2)+(
)=(x1-x2)+(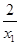 -
-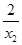 )
)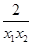 )=
)=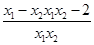 ,
,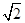 ],且x1<x2,∴x1-x2<0,0<x1x2<2.
],且x1<x2,∴x1-x2<0,0<x1x2<2.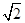 ]上是减函数,函数h(x)在(0,
]上是减函数,函数h(x)在(0,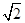 ]上的最小值是h(
]上的最小值是h(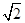 )=2
)=2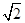 .
.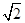 ]上的最小值是2
]上的最小值是2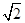 .
.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源:不详 题型:单选题
| A.f(a)<f(b) | B.f(a)>f(b) |
| C.f(a)=f(b) | D.无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com