
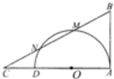
 如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.
如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.分析 (Ⅰ)设BM=x(x>0),则由切割线定理解得x=2,由勾股定理可得AC,过O作OP⊥MN于P,通过△ABC∽△POC,求出OP,得到圆心O到割线BMN的距离.
(Ⅱ)连结OM,在Rt△OPM中,求出OM,得到圆O的直径AD为$\frac{10\sqrt{7}}{7}$,从而求出CD的长.
解答 解:(Ⅰ)设BM=x(x>0),则由切割线定理可得BA2=BM•BN,又BM=MN=NC,
则(2$\sqrt{2}$)2=x(x+x),解得x=2,从而BC,
=6,由勾股定理可得AC=$\sqrt{{6}^{2}-{(2\sqrt{2})}^{2}}$=2$\sqrt{7}$.
过O作OP⊥MN于P,则CP=3,易证△ABC∽△POC,则$\frac{OP}{AB}=\frac{CP}{CA}$,所以OP=$\frac{AB•CP}{CA}$=$\frac{2\sqrt{2}×3}{2\sqrt{7}}$=$\frac{3\sqrt{14}}{7}$.
圆心O到割线BMN的距离:$\frac{3\sqrt{14}}{7}$.
(Ⅱ)连结OM,在Rt△OPM中,OM=$\sqrt{{OP}^{2}+{PM}^{2}}$=$\frac{5\sqrt{7}}{7}$.
即圆O的直径AD为$\frac{10\sqrt{7}}{7}$,从而CD的长为:2$\sqrt{7}$-$\frac{10\sqrt{7}}{7}$=$\frac{4\sqrt{7}}{7}$.
点评 本题考查推理与证明,直线与圆相交的性质的应用,考查切割线定理以及勾股定理的应用.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{6}$ | B. | $\frac{π}{6}$ | C. | $-\frac{π}{12}$ | D. | $\frac{7π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
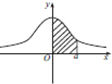 如图是正态分布N(0,1)的正态曲线图,下面4个式子中(注:Φ(a)=P(X≤a)),等于图中阴影部分的面积的个数为( )
如图是正态分布N(0,1)的正态曲线图,下面4个式子中(注:Φ(a)=P(X≤a)),等于图中阴影部分的面积的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | 8 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
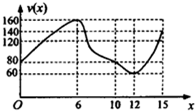 一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )
一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )| A. | 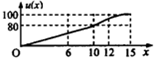 | B. | 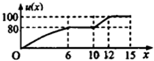 | ||
| C. | 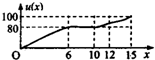 | D. | 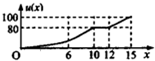 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com