已知函数f(x)=x2-(a+2)x+alnx(a∈R).
(I)求函数f(x)的单调区间;
(II)若a=4,y=f(x)的图象与直线y=m有三个交点,求m的取值范围(其中自然对数的底数e为无理数且e=2.271828…)
解:(I)函数f(x)=x
2-(a+2)x+alnx的定义域是(0,+∞).
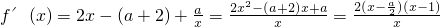
①当a≤0时,f'(x)≤0在(0,1]上恒成立,f'(x)≥0在[1,+∞)上恒成立,∴a≤0时,f(x)的增区间为[1,+∞),
f(x)的减区间为(0,1]
②当
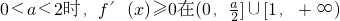
上恒成立,
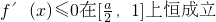
.
∴
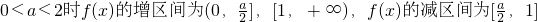
.
③当a=2时,f'(x)≥0在(0,+∞)上恒成立,∴a=2时,f(x)的增区间为(0,+∞).
④当
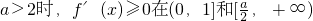
上恒成立,
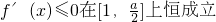
,∴

,
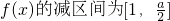
.
(II)若a=4,由(I)可得f(x)在(0,1]上单调增,在[1,2]上单调减,在[2,+∞)上单调增.
∴f(x)
极小值=f(2)=4ln2-8,f(x)
极大值=f(1)=-5
∴y=f(x)的图象与直线y=m有三个交点时m的取值范围是(4ln2-8,-5).
分析:(1)先求函数的定义域再求函数的导数,当导数大于0时函数单调递增,当导数小于0时单调递减.
(2)由a=4可根据(1)中所求确定函数的增减区间,求出函数的极小值和极大值即可得到答案.
点评:本题主要考查通过求函数的导数来确定函数的单调区间的问题.

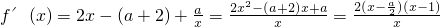
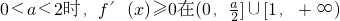 上恒成立,
上恒成立,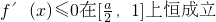 .
.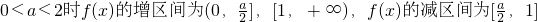 .
.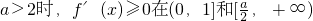 上恒成立,
上恒成立,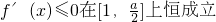 ,∴
,∴ ,
,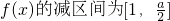 .
.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<