
【题目】设e为圆锥曲线![]() 的离心率,F为一个焦点,l是焦点所在的对称轴,O是l上距F较近的顶点,又M、N是l上满足
的离心率,F为一个焦点,l是焦点所在的对称轴,O是l上距F较近的顶点,又M、N是l上满足![]() 的两点。求证:对曲线
的两点。求证:对曲线![]() 的过点M的任一条弦AB(A、B为弦的端点),直线l平分NA和NB的一组夹角。
的过点M的任一条弦AB(A、B为弦的端点),直线l平分NA和NB的一组夹角。
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】为了解使用手机是否对学生的学习有影响,某校随机抽取100名学生,对学习成绩和使用手机情况进行了调查,统计数据如表所示(不完整):
使用手机 | 不使用手机 | 总计 | |
学习成绩优秀 | 10 | 40 | |
学习成绩一般 | 30 | ||
总计 | 100 |
(Ⅰ)补充完整所给表格,并根据表格数据计算是否有99.9%的把握认为学生的学习成绩与使用手机有关;
(Ⅱ)现从上表不使用手机的学生中按学习成绩是否优秀分层抽样选出6人,再从这6人中随机抽取3人,记这3人中“学习成绩优秀”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计,某校学生上学路程所需要时间全部介于![]() 与
与![]() 之间(单位:分钟).现从在校学生中随机抽取
之间(单位:分钟).现从在校学生中随机抽取![]() 人,按上学所学时间分组如下:第
人,按上学所学时间分组如下:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得打如图所示的频率分布直方图.
,得打如图所示的频率分布直方图.
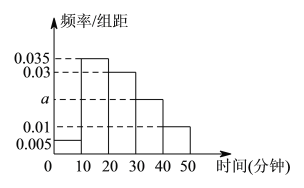
(Ⅰ)根据图中数据求![]() 的值.
的值.
(Ⅱ)若从第![]() ,
,![]() ,
,![]() 组中用分成抽样的方法抽取
组中用分成抽样的方法抽取![]() 人参与交通安全问卷调查,应从这三组中各抽取几人?
人参与交通安全问卷调查,应从这三组中各抽取几人?
(Ⅲ)在(Ⅱ)的条件下,若从这![]() 人中随机抽取
人中随机抽取![]() 人参加交通安全宣传活动,求第
人参加交通安全宣传活动,求第![]() 组至少有
组至少有![]() 人被抽中的概率.
人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,直线l与椭圆C交于A、B两点,且
,直线l与椭圆C交于A、B两点,且![]()
(1)求椭圆C的方程;
(2)若A、B两点关于原点O的对称点分别为![]() ,且
,且![]() ,判断四边形
,判断四边形![]() 是否存在内切的定圆?若存在,请求出该内切圆的方程;若不存在,请说明理由.
是否存在内切的定圆?若存在,请求出该内切圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,函数
,函数![]() ,
,![]() ,其中
,其中![]() 为常数,且
为常数,且![]() ,令函数
,令函数![]() 为函数
为函数![]() 和
和![]() 的积函数.
的积函数.
(1)求函数![]() 的表达式,并求其定义域;
的表达式,并求其定义域;
(2)当![]() 时,求函数
时,求函数![]() 的值域
的值域
(3)是否存在自然数![]() ,使得函数
,使得函数![]() 的值域恰好为
的值域恰好为![]() ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数![]() 所构成的集合;若不存在,试说明理由.
所构成的集合;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三国时代数学家赵爽在《周髀算经》中利用弦图,给出了勾股定理的绝妙证明.图中包含四个全等的直角三角形及一个小正方形(阴影),设直角三角形有一内角为![]() ,若向弦图内随机抛掷500颗米粒(大小忽略不计,取
,若向弦图内随机抛掷500颗米粒(大小忽略不计,取![]() ),则落在小正方形(阴影)内的米粒数大约为( )
),则落在小正方形(阴影)内的米粒数大约为( )
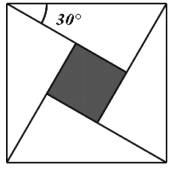
A. 134 B. 67 C. 200 D. 250
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月31日,十三届全国人大常委会第五次会议表决通过了关于修改个人所得税法的决定,这是我国个人所得税法自1980年出台以来第七次大修![]() 为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过3000元的部分 |
|
2 | 超过3000元至12000元的部分 |
|
3 | 超过12000元至25000元的部分 |
|
|
|
|
某企业员工今年10月份的月工资为15000元,则应缴纳的个人所得税为______元![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com