
����Ŀ��ij֪��Ʒ����������������ϲ�������۸�ij�����������Ƴ�A��B��C���ַ��ڸ��ʽ���۸�Ʒ�����������Խ���100λ�����������ڸ���Ŀͻ�����ͳ�Ʒ������õ����µ���״ͼ����֪��A��B��C���ַ��ڸ��������У��þ�����ÿ���۴�Ʒ������1������õ�����ֱ���1��Ԫ��2��Ԫ��3��Ԫ���ּ������˴Ӹ����������̴��������������ڸ��ʽ�������Ʒ������һ��������100λ�ͻ������õķ��ڸ��ʽ��Ƶ�ʴ���1λ�ͻ�������Ӧ���ڸ��ʽ�ĸ��ʣ�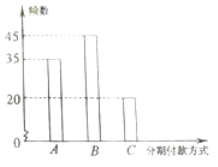
��1����������˲��ò�ͬ���ڸ��ʽ�ĸ��ʣ�
��2����X����λ����Ԫ��Ϊ�����������̴Ӽ������˹���������õ�������X�ķֲ�����������
���𰸡�
��1��
�⣺������ã�
P��A��= ![]() =0.35��P��B��=
=0.35��P��B��= ![]() =0.45��P��C��=
=0.45��P��C��= ![]() =0.2��
=0.2��
��������˲��ò�ͬ���ڸ��ʽ�ĸ��ʣ�
p=1��[P��A��P��A��+P��B��P��B��+P��C��P��C��]=0.635
��2��
�⣺��X����λ����Ԫ��Ϊ�����������̴Ӽ������˹���������õ�����
��X�Ŀ���ȡֵΪ2��3��4��5��6��
P��X=2��=P��A��P��A��=0.35��0.35=0.1225��
P��X=3��=P��A��P��B��+P��B��P��A��=0.35��0.45+0.45��0.35=0.315��
P��X=4��=P��A��P��C��+P��B��P��B��+P��C��P��A��=0.35��0.2+0.45��0.45+0.2��0.35=0.3425��
P��X=5��=P��B��P��C��+P��C��P��B��=0.45��0.2+0.2��0.45=0.18��
P��X=6��=P��C��P��C��=0.2��0.2=0.04��
��X�ķֲ���Ϊ��
X | 2 | 3 | 4 | 5 | 6 |
P | 0.1225 | 0.315 | 0.3425 | 0.18 | 0.04 |
E��X��=0.1225��2+0.315��3+0.3425��4+0.18��5+0.04��6=3.7
����������1��������ã�P��A��= ![]() =0.35��P��B��=
=0.35��P��B��= ![]() =0.45��P��C��=
=0.45��P��C��= ![]() =0.2�����ö����¼����ʼ��㹫ʽ������������˲��ò�ͬ���ڸ��ʽ�ĸ��ʣ���2����X����λ����Ԫ��Ϊ�����������̴Ӽ������˹���������õ�������X�Ŀ���ȡֵΪ2��3��4��5��6���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����
=0.2�����ö����¼����ʼ��㹫ʽ������������˲��ò�ͬ���ڸ��ʽ�ĸ��ʣ���2����X����λ����Ԫ��Ϊ�����������̴Ӽ������˹���������õ�������X�Ŀ���ȡֵΪ2��3��4��5��6���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ӹ���һ�Σ����¼�A=����������������ͬ����B=�����ٳ���һ��6�㡱�������P��A|B�����ڣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����أ�0������y=2cos����x+ ![]() ����1��ͼ������ƽ��
����1��ͼ������ƽ�� ![]() ����λ����ԭͼ���غϣ���ص���Сֵ�ǣ� ��
����λ����ԭͼ���غϣ���ص���Сֵ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��ͼ���������ԭ��Գ�.
��ͼ���������ԭ��Գ�.
��1����![]() ��ֵ��
��ֵ��
��2��������![]() ��
��![]() �ڴ�����㣬��ʵ��
�ڴ�����㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ��������ʽ
��������ʽ![]() ��
��![]() �Ϻ��������������������С����
�Ϻ��������������������С����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() ��g��x��=a2lnx+b�й����㣬���ڹ����㴦�����߷�����ͬ����ʵ��b�����ֵΪ�� ��
��g��x��=a2lnx+b�й����㣬���ڹ����㴦�����߷�����ͬ����ʵ��b�����ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]()
��1��������ʽf��x����f��x+m����1���������ʵ��m�����ֵ��
��2����a�� ![]() ʱ������g��x��=f��x��+|2x��1|����㣬��ʵ��a��ȡֵ��Χ��
ʱ������g��x��=f��x��+|2x��1|����㣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]()
��1��������ʽf��x����f��x+m����1���������ʵ��m�����ֵ��
��2����a�� ![]() ʱ������g��x��=f��x��+|2x��1|����㣬��ʵ��a��ȡֵ��Χ��
ʱ������g��x��=f��x��+|2x��1|����㣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��֪f��x��=lnx+a��1-x��,��:��1������f��x�� �ĵ����ԣ���2���� f��x�������ֵ,�����ֵ����2a-2 ʱ,��a��ȡֵ��Χ.
��֪f��x��=lnx+a��1-x��,��:��1������f��x�� �ĵ����ԣ���2���� f��x�������ֵ,�����ֵ����2a-2 ʱ,��a��ȡֵ��Χ.
��1����I������f��x�� �ĵ����ԣ�
��2����II���� f��x�������ֵ,�����ֵ����2a-2 ʱ,��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2015���Ĵ�����ͼ����ԲE��![]() ����������
����������![]() ����P��0,1���ڶ���CD�ϣ� ��
����P��0,1���ڶ���CD�ϣ� ��![]() .
.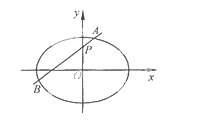
��1������ԲE�ķ��̣�
��2����OΪ����ԭ�㣬����P�Ķ�ֱ������Բ����A��B����.�Ƿ���ڳ����� �� ʹ��![]() Ϊ��ֵ�������ڣ�������ֵ���������ڣ���˵������.
Ϊ��ֵ�������ڣ�������ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com