
【题目】设ω>0,函数y=2cos(ωx+ ![]() )﹣1的图象向右平移
)﹣1的图象向右平移 ![]() 个单位后与原图象重合,则ω的最小值是( )
个单位后与原图象重合,则ω的最小值是( )
A.![]()
B.![]()
C.![]()
D.![]()
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆O1:(x+a)2+y2=4,圆O2:(x﹣a)2+y2=4,其中常数a>2,点P是圆O1 , O2外一点.
(1)若a=3,P(﹣1,4),过点P作斜率为k的直线l与圆O1相交,求实数k的取值范围;
(2)过点P作O1 , O2的切线,切点分别为M1 , M2 , 记△PO1M1 , △PO2M2的面积分别为S1 , S2 , 若S1= ![]() S2 , 求点P的轨迹方程.
S2 , 求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex(2x﹣3)﹣ax2+2ax+b,若函数 f(x)存在两个极值点x1 , x2 , 且极小值点x1大于极大值点x2 , 则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,截至2016年底全国微信注册用户数量已经突破9.27亿,为调查大学生这个微信用户群体中每人拥有微信群的数量,现从某市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量(个) | 频数 | 频率 |
0~4 | 0.15 | |
5~8 | 40 | 0.4 |
9~12 | 25 | |
13~16 | a | c |
16以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值及样本中微信群个数超过12的概率;
(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过12的概率;
(Ⅲ)以(1)中的频率作为概率,若从全市大学生中随机抽取3人,记X表示抽到的是微信群个数超过12的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1 , CC1的中点,且BE⊥B1F. 
(Ⅰ)求证:B1F⊥EC1;
(Ⅱ)求二面角C1﹣BE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.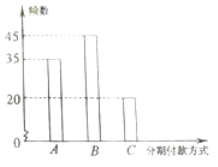
(1)求甲乙两人采用不同分期付款方式的概率;
(2)记X(单位:万元)为该汽车经销商从甲乙两人购车中所获得的利润,求X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com