
【题目】已知函数f(x)=ex﹣x2﹣ax.
(Ⅰ)若函数f(x)的图象在x=0处的切线方程为y=2x+b,求a,b的值;
(Ⅱ)若函数f(x)在R上是增函数,求实数a的最大值.
【答案】解:(Ⅰ)∵f(x)=ex﹣x2﹣ax,∴f′(x)=ex﹣2x﹣a,则f′(0)=1﹣a.
由题意知1﹣a=2,即a=﹣1.
∴f(x)=ex﹣x2+x,则f(0)=1.
于是1=2×0+b,b=1.
(Ⅱ)由题意f′(x)≥0,即ex﹣2x﹣a≥0恒成立,∴a≤ex﹣2x恒成立.
设h(x)=ex﹣2x,则h′(x)=ex﹣2.
∴当x∈(﹣∞,ln2)时,h′(x)<0,h(x)为减函数;
当x∈(ln2,+∞)时,h′(x)>0,h(x)为增函数.
∴h(x)min=h(ln2)=2﹣2ln2.
∴a≤2﹣2ln2,即a的最大值为2﹣2ln2.
【解析】(Ⅰ)求出f′(x)由f′(0)=1﹣a=2,求得a=﹣1.得到f(x)=ex﹣x2+x,再由f(0)=1求得b值;(Ⅱ)由题意f′(x)≥0,即ex﹣2x﹣a≥0恒成立,∴a≤ex﹣2x恒成立.令h(x)=ex﹣2x,利用导数求其最小值得答案.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x﹣b)(b∈R).若存在x∈[ ![]() ,2],使得f(x)+xf′(x)>0,则实数b的取值范围是( )
,2],使得f(x)+xf′(x)>0,则实数b的取值范围是( )
A.(﹣∞, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED. 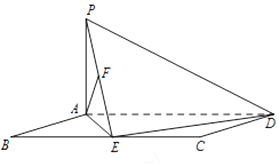
(1)求证:PA⊥平面ABCD
(2)求直线BF与平面AFD所成角的正弦值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:参数方程与极坐标系]
以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为  ,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2θ﹣2cosθ=0.
,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2θ﹣2cosθ=0.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当θ变化时,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如表:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
(Ⅰ)试分别估计芯片甲,芯片乙为合格品的概率;
(Ⅱ)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com