
| A. | $\sqrt{3}$•f($\frac{π}{6}$)>2cos1•f(1) | B. | $\sqrt{3}$f($\frac{π}{6}$)<f($\frac{π}{3}$) | C. | $\sqrt{6}$f($\frac{π}{6}$)>2f($\frac{π}{4}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>f($\frac{π}{3}$) |
分析 将条件f(x)<f'(x)tanx转化为$\frac{f'(x)sinx-f(x)cosx}{si{n}^{2}x}$>0,即($\frac{f(x)}{sinx}$)'>0,构造函数g(x)=$\frac{f(x)}{sinx}$,则g(x)在(0,$\frac{π}{2}$)上单调递增.根据单调性可知,g($\frac{π}{6}$)<g($\frac{π}{3}$),也就是$\frac{f(\frac{π}{6})}{sin\frac{π}{6}}<\frac{f(\frac{π}{3})}{sin\frac{π}{3}}$,即$\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$.
解答 解:∵f(x)<f'(x)tanx,
∴$f(x)<\frac{f'(x)sinx}{cosx}$,
∵$x∈(0,\frac{π}{2})$,∴cosx>0,
∴f'(x)sinx-f(x)cosx>0
记g(x)=$\frac{f(x)}{sinx}$,x$∈(0,\frac{π}{2})$,
则g'(x)=$(\frac{f(x)}{sinx})'=\frac{f'(x)sinx-f(x)cosx}{si{n}^{2}x}>0$,
∴$g(x)在(0,\frac{π}{2})$上单调递增,
∴$g(\frac{π}{6})<g(\frac{π}{3})$,
∴$\frac{f(\frac{π}{6})}{sin\frac{π}{6}}<\frac{f(\frac{π}{3})}{sin\frac{π}{3}}$,即$\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$.
故选:B.
点评 本题考查了利用导数研究函数的单调性,判断函数值的大小,将条件进行转化构造新函数是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
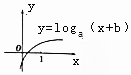 已知函数f(x)=loga(x+b)(a,b为常数)的图象如图所示,则函数g(x)=b${\;}^{{x^2}-4x}}$在[0,5]上的最大值是( )
已知函数f(x)=loga(x+b)(a,b为常数)的图象如图所示,则函数g(x)=b${\;}^{{x^2}-4x}}$在[0,5]上的最大值是( )| A. | $\frac{1}{b^4}$ | B. | $\frac{1}{b^5}$ | C. | b4 | D. | b5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4-$\sqrt{5}$ | D. | 4+$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com