
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据题意,得出函数f(x)的图象关于($\frac{π}{3}$,0)对称,也关于x=$\frac{π}{6}$对称;
由此求出函数的周期T的可能取值,从而得出ω的可能取值.
解答 解:函数f(x)=Asin(ωx+φ)满足:f($\frac{π}{3}$+x)=-f($\frac{π}{3}$-x),
所以函数f(x)的图象关于($\frac{π}{3}$,0)对称,
又f($\frac{π}{6}$+x)=f($\frac{π}{6}$-x),
所以函数f(x)的图象关于x=$\frac{π}{6}$对称;
所以$\frac{(2k-1)T}{4}$=$\frac{π}{3}$-$\frac{π}{6}$=$\frac{π}{6}$,k为正整数,
所以T=$\frac{2π}{3(2k-1)}$,
即$\frac{2π}{ω}$=$\frac{2π}{3(2k-1)}$,
解得ω=3(2k-1),k为正整数;
当k=1时,ω=3,
所以ω的一个可能取值是3.
故选:B.
点评 本题考查了函数f(x)=Asin(ωx+φ)的图象与性质的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2018,-2016) | B. | (-∞,-2018) | C. | (-2016,-2015) | D. | (-∞,-2012) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生 | 在职人员 | 退休人员 | |
| 满意 |  |  | 78 |
| 不满意 | 5 |  | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
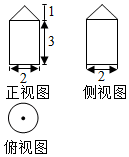
| A. | $\frac{10}{3}π$ | B. | 3π | C. | 4π | D. | $(6+\sqrt{2}π)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com