
分析 利用球面上任一点到圆面O1的距离的最大值为$\frac{3R}{2}$,可得OC=$\frac{R}{2}$,利用好截面圆的性质,勾股定理求解球的半径即可得出圆的面积.
解答 解:∵r=1,d最大=$\frac{3R}{2}$,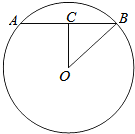
∴BC=1,OC=$\frac{R}{2}$,
∴R2=$\frac{{R}^{2}}{4}$+1,
∴R2=$\frac{4}{3}$,
∴球O的表面积为:4π×$\frac{4}{3}$=$\frac{16π}{3}$,
故答案为:$\frac{16π}{3}$.
点评 本题主要考查球的表面积的计算,根据条件求出球的半径是解决本题的关键,利用好平面图形.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
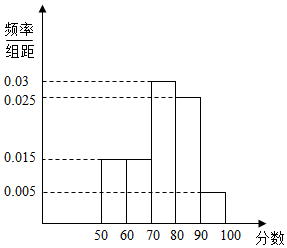
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin50°cos39°-sin40°cos51° | B. | -2sin240°+1 | ||
| C. | 2sin6°cos6° | D. | $\frac{{\sqrt{3}}}{2}sin{43°}-\frac{1}{2}cos{43°}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 5 | 0.050 |
| 第2组 | [60,70) | ① | 0.350 |
| 第3组 | [70,80) | 30 | ② |
| 第4组 | [80,90) | 20 | 0.200 |
| 第5组 | [90,100] | 10 | 0.100 |
| 合计 | ③ | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com