
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 5 | 0.050 |
| 第2组 | [60,70) | ① | 0.350 |
| 第3组 | [70,80) | 30 | ② |
| 第4组 | [80,90) | 20 | 0.200 |
| 第5组 | [90,100] | 10 | 0.100 |
| 合计 | ③ | 1.00 | |
分析 (Ⅰ)根据频率=$\frac{频数}{样本容量}$即可求出,并画出相应的图象即可,
(Ⅱ)根据分层抽样即可求出相对应的人数,
(Ⅲ)根据平均数的定义即可求出.
解答 解:(Ⅰ)5÷0.05=100,100×0.35=35,30÷100=0.030
故①35②0.300③100,其频率分布直方图如图所示:
(Ⅱ)第3,4,5组共有60名学生,第3,4,5组的频数之比为:30:20:10=3:2:1,
则第3组抽取的人数为$12×\frac{3}{6}=6$人;第4组为$12×\frac{2}{6}=4$人;第5组为$12×\frac{1}{6}=2$人.
(Ⅲ)样本平均数$\overline x=55×0.05+65×0.35+75×0.3+85×0.2+95×0.1=74.5$
点评 本题考查了频率分布直方图和分层抽样和平均数等有关问题,属于基础题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
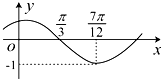
| A. | $\frac{π}{6}$ | B. | $-\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ymin=-$\frac{5}{4}$,ymax=$\frac{5}{4}$ | B. | 无最小值,ymax=$\frac{5}{4}$ | ||
| C. | ymin=-$\frac{5}{4}$,无最大值 | D. | 既无最大值也无最小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com