
分析 根据平均数与方差的计算公式,进行推导,即可求出对应的方差.
解答 解:依题意,得$\overline{x}$=$\frac{1}{5}$(x1+x2+x3+x4+x5),
∴2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的平均数为
$\overline{x′}$=$\frac{1}{5}$[(2x1+1)+(2x2+1)+(2x3+1)+(2x4+1)+(2x5+1)]
=2×$\frac{1}{5}$(x1+x2+x3+x4+x5)+1=2$\overline{x}$+1,
∵数据x1,x2,x3,x4,x5的方差为
S2=$\frac{1}{5}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+(x3-$\overline{x}$)2+(x4-$\overline{x}$)2+(x5-$\overline{x}$)2]=3,
∴数据2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的方差为
S′2=$\frac{1}{5}$[(2x1+1-2$\overline{x}$-1)2+(2x2+1-2$\overline{x}$-1)2+(2x3+1-2$\overline{x}$-1)2+(2x4+1-2$\overline{x}$-1)2+(2x5+1-2$\overline{x}$-1)2]
=$\frac{1}{5}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+(x3-$\overline{x}$)2+(x4-$\overline{x}$)2+(x5-$\overline{x}$)2]×4=3×4=12.
故答案为:12.
点评 本题考查了平均数、方差的计算.关键是熟悉计算公式,会将所求式子变形,再整体代入.


科目:高中数学 来源: 题型:解答题
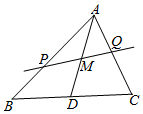 已知M为△ABC的中线AD的中点,过点M的直线分别交两边AB、AC于点P、Q,设
已知M为△ABC的中线AD的中点,过点M的直线分别交两边AB、AC于点P、Q,设查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25% | B. | 30% | C. | 40% | D. | 45% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
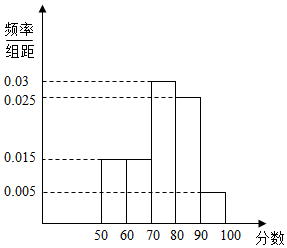
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 5 | 0.050 |
| 第2组 | [60,70) | ① | 0.350 |
| 第3组 | [70,80) | 30 | ② |
| 第4组 | [80,90) | 20 | 0.200 |
| 第5组 | [90,100] | 10 | 0.100 |
| 合计 | ③ | 1.00 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com