
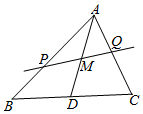
 已知M为△ABC的中线AD的中点,过点M的直线分别交两边AB、AC于点P、Q,设
已知M为△ABC的中线AD的中点,过点M的直线分别交两边AB、AC于点P、Q,设分析 (1)表示出向量AM,根据P、M、Q三点共线,得到关于x,y的等式,解出y即f(x)的解析式;
(2)分别根据f(x),g(x)的单调性,求出f(x),g(x)的值域,结合集合的包含关系得到关于a的不等式组,解出即可.
解答 解:(1)∵过点M的直线分别交两边AB、AC于P、Q,
∴0<x≤1,0<y≤1…(1分),
又∵$\overrightarrow{AP}$=x$\overrightarrow{AB}$,$\overrightarrow{AQ}$=y$\overrightarrow{AC}$,
∴$\overrightarrow{AM}$=$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{4}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{4x}$$\overrightarrow{AP}$+$\frac{1}{4y}$$\overrightarrow{AQ}$…(2分),
又∵P、M、Q三点共线,
∴$\frac{1}{4x}$+$\frac{1}{4y}$=1,
∴y=f(x)=$\frac{x}{4x-1}$…(3分),
由$\left\{\begin{array}{l}0<x≤1\\ 0<y≤1\end{array}\right.$得$\left\{\begin{array}{l}0<x≤1\\ 0<\frac{x}{4x-1}≤1\end{array}\right.$,
∴$\frac{1}{3}$≤x≤1…(4分),
∴y=f(x)=$\frac{x}{4x-1}$,x∈[$\frac{1}{3}$,1]…(5分);
(2)∵f(x)=$\frac{x}{4x-1}$=$\frac{1}{4}$+$\frac{{\frac{1}{4}}}{4x-1}$在[$\frac{1}{3}$,1]内是减函数,
∴[f(x)]min=f(1)=$\frac{1}{3}$,[f(x)]max=f($\frac{1}{3}$)=1,
即函数f(x)的值域为[$\frac{1}{3}$,1]…(7分),
∵g'(x)=3x2+3a2≥0,
∴g(x)在[0,1]内是增函数,
∴[g(x)]min=g(0)=2a,[g(x)]max=g(1)=3a2+2a+1,
∴g(x)的值域为[2a,3a2+2a+1]…(9分),
由题设得[$\frac{1}{3}$,1]⊆[2a,3a2+2a+1],
则$\left\{\begin{array}{l}{2a≤\frac{1}{3}}\\{{3a}^{2}+2a+1≥1}\end{array}\right.$ …(11分)
解得a的取值范围是(-∞,-$\frac{2}{3}$]∪[0,$\frac{1}{6}$]…(12分).
点评 本题考查了向量共线问题,考查求函数的解析式,函数的单调性、最值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 10 | 20 | 40 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com