
分析 设直线斜率为k,联立方程组得出M,N两点坐标的关系及M,N的中点坐标,求出|MN|及MN的中垂线方程,得出P点坐标,从而得出|PF|.
解答 解:椭圆的右焦点坐标为F(4,0).
设直线MN的方程为y=k(x-4).
联立方程组$\left\{\begin{array}{l}{y=k(x-4)}\\{\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1}\end{array}\right.$,消元得:(9+25k2)x2-200k2x+25(16k2-9)=0.
设M(x1,y1),N(x2,y2),MN的中点为(x0,y0),
∴x1+x2=$\frac{200{k}^{2}}{9+25{k}^{2}}$,x1x2=$\frac{25({16k}^{2}-9)}{9+25{k}^{2}}$.
x0=$\frac{1}{2}$(x1+x2)=$\frac{100{k}^{2}}{9+25{k}^{2}}$,y0=$\frac{1}{2}$(y1+y2)=$\frac{1}{2}$(x1+x2)-4k=-$\frac{36k}{9+25{k}^{2}}$.
∴MN的中垂线方程为y+$\frac{36k}{9+25{k}^{2}}$=-$\frac{1}{k}$(x-$\frac{100{k}^{2}}{9+25{k}^{2}}$),
令y=0,得x=-$\frac{36{k}^{2}}{9+25{k}^{2}}$+$\frac{100{k}^{2}}{9+25{k}^{2}}$=$\frac{64{k}^{2}}{9+25{k}^{2}}$.
∴|PF|=4-$\frac{64{k}^{2}}{9+25{k}^{2}}$=$\frac{36(1+{k}^{2})}{9+25{k}^{2}}$.
又|MN|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$$\sqrt{\frac{40000{k}^{4}}{(9+25{k}^{2})^{2}}-\frac{100(16{k}^{2}-9)}{9+25{k}^{2}}}$=$\frac{90(1+{k}^{2})}{9+25{k}^{2}}$.
∴$\frac{|PF|}{|MN|}$=$\frac{36}{90}$=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题考查了直线与椭圆的位置关系,弦长公式,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
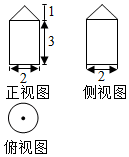
| A. | $\frac{10}{3}π$ | B. | 3π | C. | 4π | D. | $(6+\sqrt{2}π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ymin=-$\frac{5}{4}$,ymax=$\frac{5}{4}$ | B. | 无最小值,ymax=$\frac{5}{4}$ | ||
| C. | ymin=-$\frac{5}{4}$,无最大值 | D. | 既无最大值也无最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由金、银、铜、铁可导电,猜想:金属都可以导电 | |
| B. | 猜想数列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通项公式为an=$\frac{1}{n(n+1)}$(n∈N+) | |
| C. | 由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r2 | |
| D. | 半径为r圆的面积S=πr2,则单位圆的面积S=π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x3 | B. | y=|x|+1 | C. | y=-x2+4 | D. | y=($\frac{1}{2}$)|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com