
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
分析 根据题意,利用随机事件的概率公式,分别求出事件A的概率与事件A、B同时发生的概率,再用条件概率公式加以计算,可得P(B|A)的值.
解答 解:根据题意,若事件A为“x+y为偶数”发生,则x、y两个数均为奇数或均为偶数.
共有2×3×3=18个基本事件,
∴事件A的概率为P1=$\frac{2×3×3}{6×6}$=$\frac{1}{2}$.
而A、B同时发生,基本事件有“2+4”、“2+6”、“4+2”、“4+6”、“6+2”、“6+4”,
一共有6个基本事件,
因此事件A、B同时发生的概率为P2=$\frac{6}{6×6}$=$\frac{1}{6}$
因此,在事件A发生的情况下,B发生的概率为P(B|A)=$\frac{{P}_{2}}{{P}_{1}}$=$\frac{1}{3}$
故选:A.
点评 本题给出掷骰子的事件,求条件概率.着重考查了随机事件的概率公式、条件概率的计算等知识,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
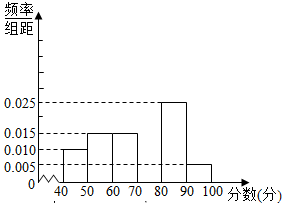 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100〕后画出如图所示的频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100〕后画出如图所示的频率分布直方图.观察图形给出的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
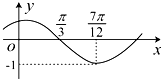
| A. | $\frac{π}{6}$ | B. | $-\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com