
分析 (I)先求出f(1)的值,直接解不等式f(1)≥2即可;
(II)若关于x的不等式f(x)≥2恒成立,利用分段函数进行求解即可求实数a的取值范围.
解答 解:(I)f(1)=|2-a|+|1-1|=|2-a|,|2-a|≥2⇒a≥4或a≤0…(4分)
(II)当a>2时,$f(x)=\left\{\begin{array}{l}3x-a-1,x>\frac{a}{2}\\-x+a-1,1≤x≤\frac{a}{2}\\-3x+a+1,x<1\end{array}\right.$
作出图象可知f(x)的最小值为$f({\frac{a}{2}})=\frac{a}{2}-1≥2⇒a≥6$,则此时a≥6;…(7分)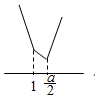
当a≤2时,$f(x)=\left\{\begin{array}{l}3x-a-1,x>1\\-x+a-1,\frac{a}{2}≤x≤1\\-3x+a+1,x<\frac{a}{2}\end{array}\right.$,作出图象可知f(x)的最
小值为$f({\frac{a}{2}})=-\frac{a}{2}+1≥2⇒a≤-2$,则此时a≤-2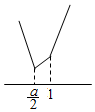
综上:a≤-2或a≥6…(10分)
点评 本题主要考查绝对值不等式的应用,根据条件表示为分段函数形式是解决本题的关键.考查学生的转化能力.


科目:高中数学 来源: 题型:解答题
 如图,矩形ABCD中,$\frac{AB}{AD}$=λ(λ>1),将其沿AC翻折,使点D到达点E的位置,且二面角C-AB-E为直二面角.
如图,矩形ABCD中,$\frac{AB}{AD}$=λ(λ>1),将其沿AC翻折,使点D到达点E的位置,且二面角C-AB-E为直二面角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
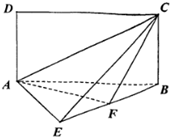
 如图,在矩形ABCD中,AB=3,BC=3$\sqrt{3}$,点E、H分别是所在边靠近B、D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD、AC、CB,形成如图所示的多面体.
如图,在矩形ABCD中,AB=3,BC=3$\sqrt{3}$,点E、H分别是所在边靠近B、D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD、AC、CB,形成如图所示的多面体.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | am>bm,则a>b | B. | a>b,则am>bm | C. | am2>bm2,则a>b | D. | a>b,则am2>bm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
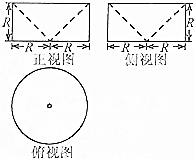
| A. | $\frac{2π{R}^{3}}{3}$ | B. | $\frac{4π{R}^{3}}{3}$ | C. | πR3 | D. | $\frac{π{R}^{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 0 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com