
| A. | y=cos$\frac{x}{2}$ | B. | y=sin($\frac{x}{2}+\frac{3π}{4}$) | C. | y=-sin(2x+$\frac{π}{4}$) | D. | y=sin(2x+$\frac{3π}{4}$) |
分析 由条件利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:将函数y=$\frac{\sqrt{2}}{2}$(sinx+cosx)=sin(x+$\frac{π}{4}$)的图象上各点的横坐标伸长到原来的2倍,可得函数y=sin($\frac{1}{2}$x+$\frac{π}{4}$)的图象;
再向左平移$\frac{π}{2}$个单位,所得函数图象的解析式为y=sin[$\frac{1}{2}$(x+$\frac{π}{2}$)+$\frac{π}{4}$]=cos$\frac{1}{2}$x,
故选:A.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.


科目:高中数学 来源: 题型:选择题
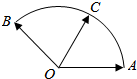 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2014}$ | B. | $\frac{1}{2015}$ | C. | $\frac{2013}{2014}$ | D. | $\frac{2014}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-$\frac{π}{4}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=-$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
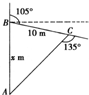 如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10m到达C处发现另一个生命迹象,这是它向右转135°可回到出发点,那么x=$\frac{10\sqrt{6}}{3}$(单位:m).
如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10m到达C处发现另一个生命迹象,这是它向右转135°可回到出发点,那么x=$\frac{10\sqrt{6}}{3}$(单位:m).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.9 | B. | 0.2 | C. | 0.7 | D. | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com