
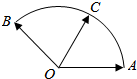
 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
分析 首先以O为原点,向量$\overrightarrow{OA}$的方向为x轴正方向,建立平面直角坐标系,并设∠COA=θ,从而可写出A,B,C三点的坐标,从而根据条件$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$便可得到$(cosθ,sinθ)=(x-\frac{y}{2},\frac{\sqrt{3}y}{2})$,这样便可得到$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{3}sinθ+cosθ}\\{y=\frac{2\sqrt{3}}{3}sinθ}\end{array}\right.$,根据两角和的正弦公式即可得到x+y=2sin(θ+30°),根据θ的范围即可得出x+y的最大值.
解答  解:如图,以O为坐标原点,直线OA为x轴,建立平面直角坐标系,则:
解:如图,以O为坐标原点,直线OA为x轴,建立平面直角坐标系,则:
A(1,0),B($-\frac{1}{2},\frac{\sqrt{3}}{2}$),设∠AOC=θ,0°≤θ≤120°,∴C(cosθ,sinθ);
∴$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}=(x,0)+(-\frac{y}{2},\frac{\sqrt{3}y}{2})$=$(x-\frac{y}{2},\frac{\sqrt{3}y}{2})=(cosθ,sinθ)$;
∴$\left\{\begin{array}{l}{x-\frac{y}{2}=cosθ}\\{\frac{\sqrt{3}y}{2}=sinθ}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{3}sinθ+cosθ}\\{y=\frac{2\sqrt{3}}{3}sinθ}\end{array}\right.$;
∴$x+y=\sqrt{3}sinθ+cosθ=2sin(θ+30°)$;
∵0°≤θ≤120°;
∴30°≤θ+30°≤150°;
∴θ+30°=90°,即θ=60°时x+y取最大值2.
故选B.
点评 考查建立平面直角坐标系利用向量坐标解决向量问题的方法,向量坐标的数乘和加法运算,以及两角和的正弦公式,正弦函数的最大值.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<3} | B. | {x|-3<x<1} | C. | {x|x<-1或x>3} | D. | {x|x>-3或x>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$ | B. | $\frac{1}{5}$ | C. | -$\frac{6}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos$\frac{x}{2}$ | B. | y=sin($\frac{x}{2}+\frac{3π}{4}$) | C. | y=-sin(2x+$\frac{π}{4}$) | D. | y=sin(2x+$\frac{3π}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com