
| A. | -$\frac{3}{5}$ | B. | $\frac{1}{5}$ | C. | -$\frac{6}{5}$ | D. | $\frac{3}{5}$ |
分析 由已知等式先将一个向量用其余两个向量表示出来,然后借助于平方使其出现向量模的平方,则才好用上外接圆半径,然后进一步分析结论,容易化简出要求的结果.
解答 解:因为3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow 0$,
所以3$\overrightarrow{OA}$+4$\overrightarrow{OB}$=-5$\overrightarrow{OC}$,
所以$9{\overrightarrow{OA}}^{2}+24\overrightarrow{OA}•\overrightarrow{OB}+16{\overrightarrow{OB}}^{2}=25{\overrightarrow{OC}}^{2}$,
因为A,B,C在圆上,所以$|\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}|=1$.
代入原式得$\overrightarrow{OA}•\overrightarrow{OB}$=0,
同理$\overrightarrow{OA}•\overrightarrow{OC}$=$-\frac{3}{5}$
所以$\overrightarrow{OA}•\overrightarrow{BC}$=$\overrightarrow{OA}•(\overrightarrow{OC}-\overrightarrow{OB})$=$\overrightarrow{OA}•\overrightarrow{OC}-\overrightarrow{OA}•\overrightarrow{OB}$=-$\frac{3}{5}$;
故选A.
点评 本题考查了平面向量在几何问题中的应用.要利用向量的三角形法则,将所求进行化归,从而将问题转化为数量积.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
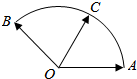 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2014}$ | B. | $\frac{1}{2015}$ | C. | $\frac{2013}{2014}$ | D. | $\frac{2014}{2015}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com