解:(Ⅰ)当n≥2时,

当n=1,a
1=S
1=1,满足上式
∴a
n=n(n∈N
*)②
(Ⅱ)由
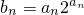
,得b
n=n•2
nT
n=2+2•2
2+3•2
3++(n-1)•2
n-1+n•2
n ①
2T
n=2
2+2•2
3+3•2
4++(n-1)•2
n+n•2
n+1 ②
①-②得,
-T
n=2+2
2+2
3++2
n-1+2
n-n•2
n+1=2
n+1-2-n•2
n+1∴T
n=(n-1)•2
n+1+2.
分析:(Ⅰ)当n≥2时,根据a
n=s
n-s
n-1,求数列{a
n}的通项公式,然后验证当n=1时,也符合上式,即可求出通项公式.
(Ⅱ)先写数列{b
n}的通项公式,然后看出数列{b
n}的前n项和T
n和2T
n,再计算出T
n-2T
n,进而可以求出前n项和T
n.
点评:本题考查了等差数列的通项公式以及数列的求和,对于等差数列与等比数列相乘形式的数列求和,一般采取错位相减的方法.

 .
.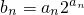 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
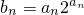 ,得bn=n•2n
,得bn=n•2n
