
【题目】某校高三某班的一次测试成绩的频率分布表以及频率分布直方图中的部分数据如下,请根据此解答如下问题: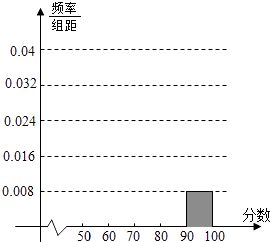
(1)求班级的总人数;
(2)将频率分布表及频率分布直方图的空余位置补充完整;
(3)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100)之间的概率.
分组 | 频数 | 频率 |
[50,60) | 0.08 | |
[60,70) | 7 | |
[70,80) | 10 | |
[80,90) | ||
[90,100) | 2 |
【答案】
(1)解:分数在[90,100)的频率为0.008×10=0.08,频数为2,
∴全班人数为 ![]() =25
=25
(2)解:[50,60)频数为2;[60,70)频率为 ![]() =0.28;[70,80)频率为
=0.28;[70,80)频率为 ![]() =0.4;[80,90)频数为4,频率为0.16,频率分布表
=0.4;[80,90)频数为4,频率为0.16,频率分布表
分组 | 频数 | 频率 |
[50,60) | 2 | 0.08 |
[60,70) | 7 | 0.28 |
[70,80) | 10 | 0.40 |
[80,90) | 4 | 0.16 |
[90,100) | 2 | 0.08 |
频率分布直方图
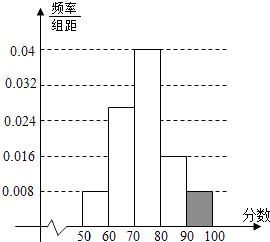 ;
;
(3)解:将[80,90)之间的频数为4,[90,100)之间的频数为2,
在[80,100)之间的试卷中任取两份的基本事件为 ![]() =15个,
=15个,
其中,至少有一个在[90,100)之间的基本事件有9个,
故至少有一份分数在[90,100)之间的概率是0.6.
【解析】(1)分数在[90,100)的频率为0.008×10=0.08,频数为2,即可求得本次考试的总人数;(2)[50,60)频数为2;[60,70)频率为 ![]() =0.28;[70,80)频率为
=0.28;[70,80)频率为 ![]() =0.4;[80,90)频数为4,频率为0.16,可得频率分布表及频率分布直方图的空余位置;(3)用列举法列举出所有的基本事件,找出符合题意得基本事件个数,利用古典概型概率计算公式即可求出结果.
=0.4;[80,90)频数为4,频率为0.16,可得频率分布表及频率分布直方图的空余位置;(3)用列举法列举出所有的基本事件,找出符合题意得基本事件个数,利用古典概型概率计算公式即可求出结果.
【考点精析】根据题目的已知条件,利用频率分布表和频率分布直方图的相关知识可以得到问题的答案,需要掌握第一步,求极差;第二步,决定组距与组数;第三步,确定分点,将数据分组;第四步,列频率分布表;频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200.220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示. (Ⅰ)求直方图中x的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为[220,240),[240,260),[260,280)的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在[220,240)的用户中应抽取多少户?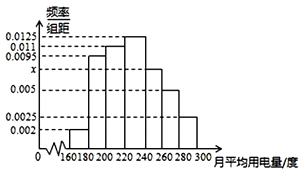
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A= ![]() ,B={y|y=log2x,4<x<16},
,B={y|y=log2x,4<x<16}, 
(1)求图中阴影部分表示的集合C;
(2)若非空集合D={x|4﹣a<x<a},且D(A∪B),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3sin(ωx+) ![]() 的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )
的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( ) 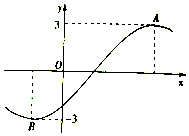
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加
平均增加![]() 个单位;
个单位;
③线性回归方程![]() 必过
必过![]() );
);
④在一个![]() 列联表中,由计算得
列联表中,由计算得![]() ,则有
,则有![]() 以上的把握认为这两个变量间有关系.
以上的把握认为这两个变量间有关系.
其中错误的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线3x+y﹣1=0上,且x轴,y轴被圆C截得的弦长分别为2 ![]() ,4
,4 ![]() ,若圆心C位于第四象限
,若圆心C位于第四象限
(1)求圆C的方程;
(2)设x轴被圆C截得的弦AB的中心为N,动点P在圆C内且P的坐标满足关系式(x﹣1)2﹣y2= ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 经过点P(2,1),且离心率为
经过点P(2,1),且离心率为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设O为坐标原点,在椭圆短轴上有两点M,N满足![]() ,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com