
【题目】已知圆C的圆心在直线3x+y﹣1=0上,且x轴,y轴被圆C截得的弦长分别为2 ![]() ,4
,4 ![]() ,若圆心C位于第四象限
,若圆心C位于第四象限
(1)求圆C的方程;
(2)设x轴被圆C截得的弦AB的中心为N,动点P在圆C内且P的坐标满足关系式(x﹣1)2﹣y2= ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:设圆C的方程为:(x﹣a)2+(y﹣b)2=r2,
根据题意,有 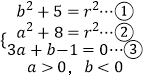
①﹣②得b2=a2+3,…④
由③④得4a2﹣3a﹣1=0,∵a>0,解得a=1,b=1﹣3a=﹣2,r2=9,
∴圆C的方程为:(x﹣1)2+(y+2)2=9,
(2)解:在圆C的方程:(x﹣1)2+(y+2)2=9中令y=0,
得A(1﹣ ![]() ,0),B(1+
,0),B(1+ ![]() ),∴N(1,0).
),∴N(1,0).
∵动点P(x,y)在圆C内,∴(x﹣1)2+(y+2)2<9…①
将①代入(x﹣1)2﹣y2= ![]() 得﹣
得﹣ ![]() ,0
,0 ![]()
![]() =(1﹣
=(1﹣ ![]() ﹣x,﹣y)(1+
﹣x,﹣y)(1+ ![]() ﹣x,﹣y)=(x﹣1)2+y2﹣5…②
﹣x,﹣y)=(x﹣1)2+y2﹣5…②
将(x﹣1)2﹣y2= ![]() 代入②得
代入②得 ![]() =2y2﹣
=2y2﹣ ![]() .
.
【解析】(1)设圆C的方程为:(x﹣a)2+(y﹣b)2=r2 , 根据题意,有 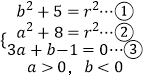
由①②③得a=1,b=1﹣3a=﹣2,r2=9,即可得圆的方程;(2)在圆C的方程:(x﹣1)2+(y+2)2=9中令y=0,得A(1﹣ ![]() ,0),B(1+
,0),B(1+ ![]() ),N(1,0).
),N(1,0).
将x﹣1)2+(y+2)2<9.(x﹣1)2﹣y2= ![]() 代入
代入 ![]() =(1﹣
=(1﹣ ![]() ﹣x,﹣y)(1+
﹣x,﹣y)(1+ ![]() ﹣x,﹣y)=(x﹣1)2+y2﹣5即可求解.
﹣x,﹣y)=(x﹣1)2+y2﹣5即可求解.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),设
为参数),设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时, ![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)写出![]() 的普遍方程及参数方程;
的普遍方程及参数方程;
(2)以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,设曲线
轴正半轴为极轴建立极坐标系,设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如表:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为: S= 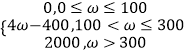 ,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关? 附:
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
k2= ![]()
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三某班的一次测试成绩的频率分布表以及频率分布直方图中的部分数据如下,请根据此解答如下问题: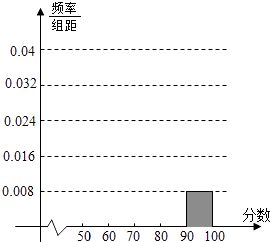
(1)求班级的总人数;
(2)将频率分布表及频率分布直方图的空余位置补充完整;
(3)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100)之间的概率.
分组 | 频数 | 频率 |
[50,60) | 0.08 | |
[60,70) | 7 | |
[70,80) | 10 | |
[80,90) | ||
[90,100) | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有1000个座位,票价不分等次,根据影院的经营经验,当每张票价不超过10元时,票可全售出;当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院定一个合适的票价,需符合的基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放一场电影的成本费用支出为5750元,票房的收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入) 问:
(1)把y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,票价定为多少时,放映一场的净收人最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的机坐标系中,直线
轴的非负半轴为极轴建立的机坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() 两点,求点
两点,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是双曲线 ![]() =1(a>0,b>0)的左,右焦点,点F1关于渐近线的对称点恰好在以F2为圆心,|OF2|(O为坐标原点)为半径的圆上,则该双曲线的离心率为 .
=1(a>0,b>0)的左,右焦点,点F1关于渐近线的对称点恰好在以F2为圆心,|OF2|(O为坐标原点)为半径的圆上,则该双曲线的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在其定义区间[a,b]上满足①f(x)>0;②f′(x)<0;③对任意的x1 , x2∈[a,b],式子 ![]() ≤
≤ ![]() 恒成立.记S1=
恒成立.记S1= ![]() f(x)dx,S2=
f(x)dx,S2= ![]() (b﹣a),S3=f(b)(b﹣a),则S1 , S2 , S3的大小关系为 . (按由小到大的顺序)
(b﹣a),S3=f(b)(b﹣a),则S1 , S2 , S3的大小关系为 . (按由小到大的顺序)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com