
【题目】某高校在上学期依次举行了“法律、环保、交通”三次知识竞赛活动,要求每位同学至少参加一次活动.该高校2014级某班50名学生在上学期参加该项活动的次数统计如图所示. 
(1)从该班中任意选两名学生,求他们参加活动次数不相等的概率.
(2)从该班中任意选两名学生,用ξ表示这两人参加活动次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
(3)从该班中任意选两名学生,用η表示这两人参加活动次数之和,记“函数f(x)=x2﹣ηx﹣1在区间(3,5)上有且只有一个零点”为事件A,求事件A发生的概率.
【答案】
(1)解:从该班任取两名学生,他们参加活动的次数恰好相等的概率:
P= ![]() =
= ![]() ,故P=1﹣
,故P=1﹣ ![]() =
= ![]()
(2)解:从该班中任选两名学生,用ξ表示这两学生参加活动次数之差的绝对值,则ξ的可能取值分别为:0,1,2,
于是P(ξ=0)= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,从而ξ的分布列为:
,从而ξ的分布列为:
ξ | 0 | 1 | 2 |
P |
|
|
|
Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =
= ![]()
(3)解:因为函数f(x)=x2﹣ηx﹣1 在区间(3,5)上有且只有一个零点,则
f(3)f(5)<0,即:(8﹣3η)(24﹣5η)<0,
∴ ![]() <η<
<η< ![]() ,
,
又由于η的取值分别为:2,3,4,5,6,故η=3或4,
故所求的概率为:P(A)= ![]() =
= ![]()
【解析】( 1)由图可知,参加活动1次、2次和3次的学生人数分别为5、25和20.由此能求出从该班中任选两名学生,他们参加活动次数恰好相等的概率,继而求出不等的概率;.(2)从该班中任选两名学生,用ξ表示这两学生参加活动次数之差的绝对值,则ξ的可能取值分别为:0,1,2由此能求出ξ的分布列和ξ的数学期望;(3)根据函数零点定理,可得f(3)f(5)<0,求出η的值,再根据古典概率求出事件A发生的概率.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,且AB=AD,BC=DC.
(1)求证:![]() ∥平面EFGH;
∥平面EFGH;
(2)求证:四边形EFGH是矩形.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为ρ=2cosθ,直线l的参数方程为 ![]() (t为参数,α为直线的倾斜角).
(t为参数,α为直线的倾斜角).
(I)写出直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C有唯一的公共点,求角α的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两个投资项目的利润率分别为随机变量X1和X2,根据市场分析,X1和X2的分布列分别为
X1 | 5% | 10% |
P | 0.8 | 0.2 |
X2 | 2% | 8% | 12% |
P | 0.2 | 0.5 | 0.3 |
(1)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差V(Y1)、V(Y2);
(2)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品有4件正品和2件次品混在了一起,现要把这2件次品找出来,为此每次随机抽取1件进行测试,测试后不放回,直至次品全部被找出为止.
(1)求“第1次和第2次都抽到次品”的概率;
(2)设所要测试的次数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产一种品牌服装的年固定成本为10万元,且每生产1万件,需要另投入1.9万元.设R(x)(单位:万元)为销售收入,根据市场调查知R(x)= 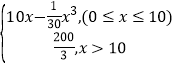 其中x(单位:万件)是年产量.
其中x(单位:万件)是年产量.
(1)写出年利润W(单位:万元)关于年产量x的函数解析式.
(2)当年产量为多少时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如图所示的频率分布直方图.

(1)求这500件产品质量指标值的样本平均数![]() 和样本方差s2(同一组中的数据用该组区间的中点值作代表).
和样本方差s2(同一组中的数据用该组区间的中点值作代表).
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2.
,σ2近似为样本方差s2.
①利用该正态分布,求P(187.8<Z<212.2);
②某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)上的产品件数,利用①的结果,求E(X).
附:![]() ≈12.2.
≈12.2.
若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com