
【题目】设![]() 、
、![]() 为曲线
为曲线![]() :
:![]() 上两点,
上两点,![]() 与
与![]() 的横坐标之和为
的横坐标之和为![]() .
.
(1)求直线![]() 的斜率;
的斜率;
(2)![]() 为曲线
为曲线![]() 上一点,
上一点,![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,且
平行,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)1;(2)![]()
【解析】
试题分析:(1)由直线斜率公式可得AB的斜率![]() ,再根据A与B的横坐标之和为4,得AB的斜率
,再根据A与B的横坐标之和为4,得AB的斜率![]() .(2)先根据导数几何意义得M点坐标,再根据直角三角形性质得
.(2)先根据导数几何意义得M点坐标,再根据直角三角形性质得![]() ,(AB的中点为N),设直线AB的方程为
,(AB的中点为N),设直线AB的方程为![]() ,与抛物线方程联立,利用两点间距离公式以及弦长公式可得关系式
,与抛物线方程联立,利用两点间距离公式以及弦长公式可得关系式![]() ,解得
,解得![]() .即得直线AB的方程为
.即得直线AB的方程为![]() .
.
试题解析:解:(1)设A(x1,y1),B(x2,y2),则![]() ,
,![]() ,
,![]() ,x1+x2=4,
,x1+x2=4,
于是直线AB的斜率![]() .
.
(2)由![]() ,得
,得![]() .
.
设M(x3,y3),由题设知![]() ,解得
,解得![]() ,于是M(2,1).
,于是M(2,1).
设直线AB的方程为![]() ,故线段AB的中点为N(2,2+m),|MN|=|m+1|.
,故线段AB的中点为N(2,2+m),|MN|=|m+1|.
将![]() 代入
代入![]() 得
得![]() .
.
当![]() ,即
,即![]() 时,
时,![]() .
.
从而![]() .
.
由题设知![]() ,即
,即![]() ,解得
,解得![]() .
.
所以直线AB的方程为![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6 ![]() ,则BC的长为 .
,则BC的长为 . 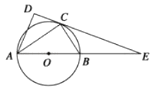
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() ﹣…+
﹣…+ ![]() ﹣
﹣ ![]() +
+ ![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.f(x)在(0,1)上恰有一个零点
B.f(x)在(0,1)上恰有两个零点
C.f(x)在(﹣1,0)上恰有一个零点
D.f(x)在(﹣1,0)上恰有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点. 
(1)求异面直线AB与EF所成角的余弦值;
(2)求E到平面ACD的距离;
(3)求EF与平面ACD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若ξ服从正态分布N(0,2),且P(ξ>2)=0.4,则P(0<ξ<2)=0.2
B.x=1是x2﹣x=0的必要不充分条件
C.直线ax+y+2=0与ax﹣y+4=0垂直的充要条件为a=±1
D.“若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个不透明的箱子里放有四个质地相同的小球,四个小球标的号码分别为1,1,2,3.现甲、乙两位同学依次从箱子里随机摸取一个球出来,记下号码并放回.
(Ⅰ)求甲、乙两位同学所摸的球号码相同的概率;
(Ⅱ)求甲所摸的球号码大于乙所摸的球号码的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系原点O为极点,以x轴非负半轴为极轴,以平面直角坐标系的长度单位为长度单位建立极坐标系.已知直线l的参数方程为 ![]() (t为参数),曲线C的极坐标方程为ρsin2θ=4cosθ
(t为参数),曲线C的极坐标方程为ρsin2θ=4cosθ
(Ⅰ) 求曲线C的直角坐标方程;
(Ⅱ) 设直线l与曲线C相交于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若图所示,将若干个点摆成三角形图案,每条边(包括两个端点)n(n>1,n∈N*)个点,相应的图案中总的点数记为an , 则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() = .
= . 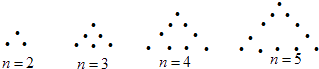
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com