练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知是直线上的动点，是圆的切线，是切点， 是圆心，那么四边形面积的最小值是(    ). 

    A．                        B．            C．          D．


    C

    【解析】


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设α为第四象限的角，若，则tan2α=        .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若Sn和Tn分别表示数列{an}和{bn}的前n项和，对任意正整数an=-2(n+1),Tn-3S­=4n.

    (Ⅰ)求数列{bn}的通项公式；

    （Ⅱ）在平面直角坐标系内，直线ln的斜率为bn.且与曲线y=x2有且仅一个交点，与y轴交于Dn，记dn=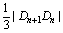-(2n+7)求dn;

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在坐标平面上，不等式组所表示的平面区域的面积为  (   )

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    曲线C：

       

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若圆C:关于直线对称，则由点向圆所作的切线长的最小值是（   ）

    A. 2      B.  3         C.  4       D.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    圆心在抛物线x2=2y上，与直线2x+2y+3=0相切的圆中，面积最小的圆的方程为                ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，直四棱柱ABCD—A1B1C1D1的底面ABCD为平行四边形，其中AB=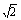，BD=BC=1，AA1=2，E为DC中点，点F在DD1上，且DF=。

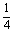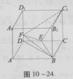
    （1）求异面直线BD与A1D1的距离；

    （2）EF与BC1是否垂直？请说明理由；

    （3）求二面角E—FB—D的正切值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    四棱锥P=ABCD中，AB⊥CD，CD⊥AD，PA⊥底面ABCD，PA=AD=CD=2AB=2，M为PC的中点。

    （1）求证BM∥平面PAD； 

    （2）在△PAD内找一点N，使MN⊥平面PBD；

    （3）求直线PC与平面PBD所成角的正弦值。

    查看答案和解析>>

    同步练习册答案