练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，直四棱柱ABCD—A1B1C1D1的底面ABCD为平行四边形，其中AB=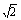，BD=BC=1，AA1=2，E为DC中点，点F在DD1上，且DF=。

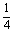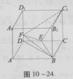
    （1）求异面直线BD与A1D1的距离；

    （2）EF与BC1是否垂直？请说明理由；

    （3）求二面角E—FB—D的正切值。


    同正解一；

    由已知可得∠ADB=90°，DD1⊥平面ABCD，∴以、、分别为x,轴y轴,z轴的正方向，建立空间坐标系，F（0，0，）、E（）、A（1，0，0）、D1（0，0，2），∴=  =（-1，0，2）又BC1∥AD1，∴EF⊥AD1。

    可以得平面BDF的一个法向量为=（-1，0，0），B（0，1，0），设平面BEF的一个法向量为n=(x,y,z)由n⊥,令x=1,得y=-1,z=-4, ∴平面BEF的一个法向量为n=（1，-1，-4），∴cosα=，∴所求二面角E—FB—D的大小为arccos


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    极限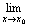f(x)存在是函数f(x)在点x=x0处连续的   （ ）

    A．充分而不必要的条件

    B．必要而不充分的条件

    C．充要条件

    D．既不充分也不必要的条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知是直线上的动点，是圆的切线，是切点， 是圆心，那么四边形面积的最小值是(    ). 

    A．                        B．            C．          D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过点，且在y轴上的截距是在x轴上的截距的2倍的直线方程是           （    ）

    A．            B．或    

    C．              D．或

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图10-15，在棱长为4的正方体ABCD—A1B1C1D1中，O是正方形A1B1C1D1的中心，点P在棱CC1上，且CC1=4CP。

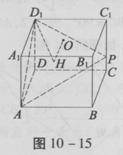
    （1）求直线AP与平面BCC1B1所成角的大小（结果用反三角表示）；

    （2）设O点在平面D1AP上的射影为H，求证：D1H⊥AP；

    （3）求点P到平面ABD1的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


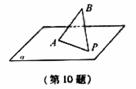
    如图，AB是平面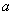的斜线段，A为斜足，若点P在平面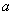内运动，使得△ABP的面积为定值，则动点P的轨迹是

    A.圆                      B.椭圆        

    C.一条直线                D.两条平行直线

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，直三棱柱ABC—A1B1C1中，∠ACB=90°，BC=AC=2，AA1=4，D为棱CC1上一动点，M、N分别为△ABD、△A1B1R的重心。

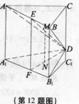
    （1）求证：MN⊥BC；

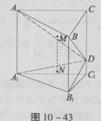
    （2）若二面角C—AB—D的大小为arctan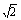,求C1到平面A1B1D的距离；

    （3）若点C在平面ABD上的射影恰好为M，试判断点C1在平面A1B1D上的射影是否为N？并说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正三棱柱ABC-A1B1C1中，D是AC的中点，AB1⊥BC1，则平面DBC1积与平面CBC1所成的角为   （  ）

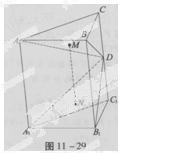
    A．30°        B．45°        C．60°        D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    以下茎叶图记录了甲、乙两组各四名同学的植树棵数．乙组记录中有一个数据模糊，无法确认，在图中以X表示．

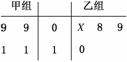
    (1)如果X＝8，求乙组同学植树棵数的平均数和方差；

    (2)如果X＝9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率．

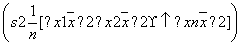
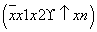
    查看答案和解析>>

    同步练习册答案