
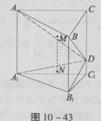
如图,直三 棱柱ABC—A1B1C1中,∠ACB=90°,BC=AC=2,AA1=4,D为棱CC1上一动点,M、N分别为△ABD、△A1B1R的重心。
棱柱ABC—A1B1C1中,∠ACB=90°,BC=AC=2,AA1=4,D为棱CC1上一动点,M、N分别为△ABD、△A1B1R的重心。
(1)求证:MN⊥BC;
(2)若二面角C—AB—D的大小为arctan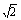 ,求C1到平面A1B
,求C1到平面A1B 1D的距离;
1D的距离;
(3)若点C在平面ABD上的射影恰好为M,试判断点C1在平面A1B1D上的射影是否为N?并说明理由。
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
若Sn和Tn分别表示数列{an}和{bn}的前n项和,对任意正整数an=-2(n+1),Tn-3S=4n.
(Ⅰ)求数列{bn}的通项公式;
( Ⅱ)在平面直角坐标系内,直线ln的斜率为bn.且与曲线y=x2有且仅一个交点,与y轴交于Dn,记dn=
Ⅱ)在平面直角坐标系内,直线ln的斜率为bn.且与曲线y=x2有且仅一个交点,与y轴交于Dn,记dn=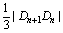 -(2n+7)求dn;
-(2n+7)求dn;
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,直四棱柱ABCD—A1B1C1D1的底面ABCD为平行四边形,其中AB=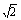 ,BD=BC=1,AA1=2,E为DC中点,点F在DD1上,且DF=
,BD=BC=1,AA1=2,E为DC中点,点F在DD1上,且DF=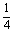 。
。
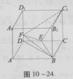
(1)求异面直线BD与A1D1的距离;
(2)EF与BC1是否垂直?请说明理由;
(3)求二面角E—FB—D的正切值。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在正四棱锥S—ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总有PE⊥AC。
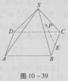
(1)证明SB⊥AC;
(2)指出动点P的轨迹,并证明你的结论;
(3)以轨迹上的动点P为顶点的三棱锥P—CDE的最大体积为V1,正四棱锥S—ABCD的体积为V,则V1:V等于多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
如图11-14,已知三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC、△PEF都是正三角形,PF⊥AB。
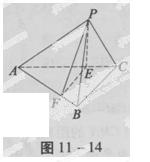
(1)证明:PC⊥平面PAB;
(2)求二面角P-AB-C的平面角的余弦值;
(3)若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长。
查看答案和解析>>
科目:高中数学 来源: 题型:
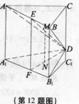
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD,如图11-12。
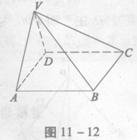
(1)证明:AB⊥平面VAD;
(2)求二面角A-VD-B的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
四棱锥P=ABCD中,AB⊥CD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
(1)求证BM∥平面PAD;
(2)在△PAD内找一点N,使MN⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com