如图10-15，在
棱长为4的正方体ABCD—A1B1C1D1中，O是正方形A1B1C1D1的中心，点P在棱CC1上，且CC1=4CP。
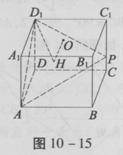
（1）求直线AP与平面BCC1B1所成角的大小（结果用反三角表示）；
（2）设O点在平面D1AP上的射影为H，求证：D1H⊥AP；
（3）求点P到平面ABD1的距离。
科目：高中数学 来源： 题型：
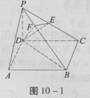
如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB于点F.
（1）证明：PA//平面EDB；
（2）证明：BP⊥平面EFD；
（3）求二面角C—PD—D的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
如图，直四棱柱ABCD—A1B1C1D1的底面ABCD为平行四边形，其中AB=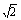
，BD=BC=1，AA1=2，E为DC中点，点F在DD1上，且DF=
。
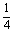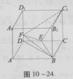
（1）求异面直线BD与A1D1的距离；
（2）EF与BC1是否垂直？请说明理由；
（3）求二面角E—FB—D的正切值。
查看答案和解析>>
科目：高中数学 来源： 题型：
如图，在正四棱锥S—ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总有PE⊥AC。
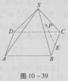
（1）证明SB⊥AC；
（2）指出动点P的轨迹，并证明你的结论；
（3）以轨迹上的动点P为顶点的三棱锥P—CDE的最大体积为V1，正四棱锥S—ABCD的体积为V，则V1：V等于多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD，如图11-12。
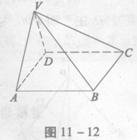
（1）证明：AB⊥平面VAD；
（2）求二面角A-VD-B的大小。
查看答案和解析>>
科目：高中数学 来源： 题型：
某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生．为了解学生的就业倾向，用分层抽样的方法从该校这四个专业共抽取40名学生进行调查，应在丙专业抽取的学生人数为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
正解二：（1）以
、
、
分别为x轴、y轴、z轴的正方向建立空间坐标系，∵AB⊥平面BCC1B1，
1)}(n∈N*) 为等差数列，且a1=3,a2=5,则
= ( )
C．1 D．
