练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

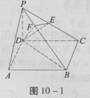
    如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB于点F.

    （1）证明：PA//平面EDB；

    （2）证明：BP⊥平面EFD；

    （3）求二面角C—PD—D的大小.


    2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图所示，有一农民在自留地建造一个长10 m，深0．5 m，横截面为等腰梯形的封闭式引水槽侧面材料每平方米造价50元，顶盖材料每平方米造价10元．

     (1)把建立引水槽的费用y(元)表示为引水槽的侧面与地面所成的角∠DAE=θ的函数；

     (2)引水槽的侧面与地面所成的角θ多大时，其材料费最低?最低材料费是多少?(精确到0．01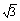，≈1．732)

     (3)按照题没条件，在引水槽的深度和横截面积及所在的材料不改变的情况下，将引水槽的横截面形状改变为正方形时的材料费与(2)中所求得的材料费相比较，哪一种设计所用材料费更省?省多少?

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    △ABC的外接圆的圆心为O，两条边上的高的交点为H.则实数m=______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    圆心在曲线 上，且与直线相切的面积最小的圆的方程为（　　）

    A．　　　　　　　B．

    C．    　　　 D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    经过点作圆的弦，使得点平分弦，则弦所在直线的方程为               ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


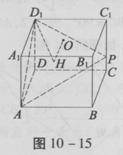
    如图10-15，在棱长为4的正方体ABCD—A1B1C1D1中，O是正方形A1B1C1D1的中心，点P在棱CC1上，且CC1=4CP。

    （1）求直线AP与平面BCC1B1所成角的大小（结果用反三角表示）；

    （2）设O点在平面D1AP上的射影为H，求证：D1H⊥AP；

    （3）求点P到平面ABD1的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知平面α⊥平面β，α∩β= l，点A∈α，A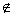l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（    ）

    A. AB∥m        B. AC⊥m    C. AB∥β   D. AC⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在如图的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC，BC＝2AD＝4，EF＝3，AE＝BE＝2，G是BC的中点．

     (1)求证：AB∥平面DEG；

    (2)求证：BD⊥EG；

    (3)求二面角C－DF－E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝6x－4(x＝1,2,3,4,5,6)的值域为集合A，函数g(x)＝2x－1(x＝1,2,3,4,5,6)的值域为集合B，任意x∈A∪B，则x∈A∩B的概率是________．

    查看答案和解析>>

    同步练习册答案