
已知平面α⊥平面β,α∩β = l,点A∈α,A
= l,点A∈α,A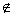 l,直线AB∥l,直线AC⊥l,直线m∥α
l,直线AB∥l,直线AC⊥l,直线m∥α ,m∥β,则下列四种位置关系中,不一定成立的是( )
,m∥β,则下列四种位置关系中,不一定成立的是( )
A. AB∥m B. AC⊥m C. AB∥β D. AC⊥β
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知un=an-1b+an-2b2+…+abn-1+bn(n∈N*,a>0,b>0).
(Ⅰ)当a=b时,求数列{un}的前项n项和Sn。
(Ⅱ)求
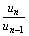 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
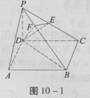
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点F.
(1)证明:PA//平面EDB;
(2)证明:BP⊥平面EFD;
(3)求二面角C—PD—D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
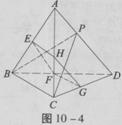
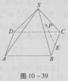
如图10-4所示,在正三棱锥A—BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于E、F、G、H。
(1)判定四边形EFGH的形状,并说明理由;
(2)设P是棱AD上的点,当AP为何值时,平面PBC⊥平面EFGH,请给出证明。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在正四棱锥S—ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总有PE⊥AC。
(1)证明SB⊥AC;
(2)指出动点P的轨迹,并证明你的结论;
(3)以轨迹上的动点P为顶点的三棱锥P—CDE的最大体积为V1,正四棱锥S—ABCD的体积为V,则V1:V等于多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
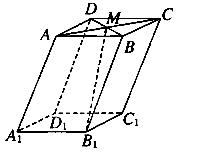
如图,在底面ABCD为平行四边形的四棱柱ABCD-A1B1C1D1中,M是AC与BD的交点,若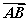 =a,
=a,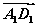 =b,
=b,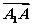 =c则下列向量中与
=c则下列向量中与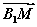 相等的向量是( )
相等的向量是( )
A.- a+
a+ b+c B.
b+c B. a+
a+ b+c
b+c
C. a-
a- b+
b+ c D.-
c D.- a-
a- b+c
b+c
查看答案和解析>>
科目:高中数学 来源: 题型:
甲和乙等五名志愿者被随机地分到A、B、C、 D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )
D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )
(A) 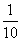 (B)
(B) 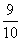 (C)
(C) 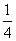
 (D)
(D) 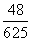
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com