练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

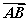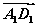    如图，在底面ABCD为平行四边形的四棱柱ABCD－A1B1C1D1中，M是AC与BD的交点，若＝a，＝b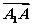，＝c则下列向量中与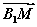相等的向量是(　　)

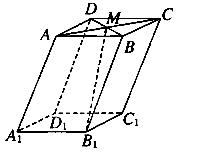
    A．－a＋b＋c           B.a＋b＋c

    C.a－b＋c                                 D．－a－b＋c


    A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    △ABC的外接圆的圆心为O，两条边上的高的交点为H.则实数m=______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知平面α⊥平面β，α∩β= l，点A∈α，A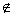l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（    ）

    A. AB∥m        B. AC⊥m    C. AB∥β   D. AC⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：


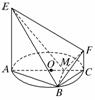
    在如图的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC，BC＝2AD＝4，EF＝3，AE＝BE＝2，G是BC的中点．

     (1)求证：AB∥平面DEG；

    (2)求证：BD⊥EG；

    (3)求二面角C－DF－E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正方体ABCD-A1B1C1D1中，M、N分别是棱AA1和BB1的中点，则CM与D1N夹角的正弦值为  （  ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


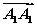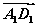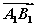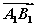    已知ABCD－A1B1C1D1为正方体，①(＋＋)2＝32；②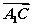·(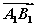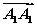－)＝0；③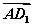向量与向量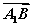的夹角是60°；④正方体ABCD－A1B1C1D1的体积为|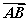··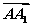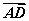|.其中正确命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    四棱锥P-ABCD中，底面ABCD是一个平行四边形，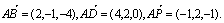

    （1）求证：PA⊥底面ABCD；

    （2）求四棱锥P-ABCD的体积；

    （3）对于向量a=（x1,y1,z1）.b=(x2,y2,z2),c=(x3,y3,z3)定义一种运算：

    （a×b）·c=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1试计算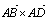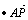（）的绝对值的值；说明其与四棱锥P-ABCD体积的关系，并同此猜想这一运算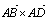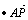（）的绝对值的几何意义。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝6x－4(x＝1,2,3,4,5,6)的值域为集合A，函数g(x)＝2x－1(x＝1,2,3,4,5,6)的值域为集合B，任意x∈A∪B，则x∈A∩B的概率是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用数学归纳法证明：“(n＋1)·(n＋2)·…·(n＋n)＝2n·1·3·…·(2n－1)”．从“k到k＋1”左端需增乘的代数式为(　　)

    A．2k＋1         B．2(2k＋1)        C.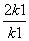         D.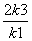

    查看答案和解析>>

    同步练习册答案