
ΥΡάβΉΕP-ABCD÷–Θ§ΒΉΟφABCD «“ΜΗωΤΫ––ΥΡ±Ώ–ΈΘ§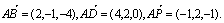
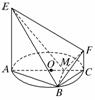 Θ®1Θ©«σ÷ΛΘΚPAΓΆΒΉΟφABCDΘΜ
Θ®1Θ©«σ÷ΛΘΚPAΓΆΒΉΟφABCDΘΜ
Θ®2Θ©«σΥΡάβΉΕP-ABCDΒΡΧεΜΐΘΜ
Θ®3Θ©Ε‘”ΎœρΝΩa=Θ®x1,y1,z1Θ©.b=(x2,y2,z2),c=(x3,y3,z3 )Ε®“ε“Μ÷÷‘ΥΥψΘΚ
)Ε®“ε“Μ÷÷‘ΥΥψΘΚ
Θ®aΓΝbΘ©·c=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1 ‘ΦΤΥψΘ®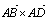 Θ©
Θ©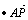 ΒΡΨχΕ‘÷ΒΒΡ÷ΒΘΜΥΒΟςΤδ”κΥΡάβΉΕP-ABCDΧεΜΐΒΡΙΊœΒΘ§≤ΔΆ§¥Υ≤¬œκ’β“Μ‘ΥΥψΘ®
ΒΡΨχΕ‘÷ΒΒΡ÷ΒΘΜΥΒΟςΤδ”κΥΡάβΉΕP-ABCDΧεΜΐΒΡΙΊœΒΘ§≤ΔΆ§¥Υ≤¬œκ’β“Μ‘ΥΥψΘ®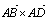 Θ©
Θ©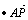 ΒΡΨχΕ‘÷ΒΒΡΦΗΚΈ“β“εΓΘ
ΒΡΨχΕ‘÷ΒΒΡΦΗΚΈ“β“εΓΘ
 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
‘ΎΥΡΟφΧεABCD÷–Θ§CB=CDΘ§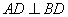 Θ§
Θ§
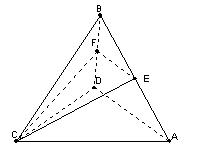
«“EΘ§FΖ÷±π «ABΘ§BDΒΡ÷–ΒψΘ§
«σ÷ΛΘ®IΘ©÷±œΏ ΘΜ
ΘΜ
Θ®IIΘ©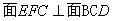 ΓΘ
ΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
»γΆΦΘ§‘ΎΒΉΟφABCDΈΣΤΫ––ΥΡ±Ώ–ΈΒΡΥΡάβ÷υABCDΘ≠A1B1C1D1÷–Θ§M «AC”κBDΒΡΫΜΒψΘ§»τ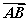 ΘΫaΘ§
ΘΫaΘ§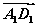 ΘΫbΘ§
ΘΫbΘ§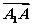 ΘΫc‘ρœ¬Ν–œρΝΩ÷–”κ
ΘΫc‘ρœ¬Ν–œρΝΩ÷–”κ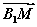 œύΒ»ΒΡœρΝΩ «(ΓΓΓΓ)
œύΒ»ΒΡœρΝΩ «(ΓΓΓΓ)
AΘ°Θ≠ aΘΪ
aΘΪ bΘΪc B.
bΘΪc B. aΘΪ
aΘΪ bΘΪc
bΘΪc
C. aΘ≠
aΘ≠ bΘΪ
bΘΪ c DΘ°Θ≠
c DΘ°Θ≠ aΘ≠
aΘ≠ bΘΪc
bΘΪc
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
…ηœρΝΩaΘΫ(3,5Θ§Θ≠4)Θ§bΘΫ(2,1,8)Θ§ΦΤΥψ2aΘΪ3b,3aΘ≠2bΘ§a·b“‘ΦΑa”κbΥυ≥…Ϋ«ΒΡ”ύœ“÷ΒΘ§≤Δ»ΖΕ®ΠΥΘ§ΠΧ”Π¬ζΉψΒΡΧθΦΰΘ§ ΙΠΥaΘΪΠΧb”κz÷α¥Ι÷±Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
Ρ≥»Υ”–5Α―‘Ω≥ΉΘ§Τδ÷–”–1Α―Ω…“‘¥ρΩΣΖΩΟ≈Θ§ΒΪΆϋΦ«ΝΥΩΣΟ≈ΒΡ «ΡΡ“ΜΑ―Θ§”Ύ «Υϊ÷πΑ―≤Μ÷ΊΗ¥ΒΊ ‘ΩΣΘ§Ρ«Ο¥«ΓΚΟΒΎ»ΐ¥Έ¥ρΩΣΖΩΟ≈ΒΡΗ≈¬ «____________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
…ηΥφΜζ±δΝΩΖΰ¥”’ΐΧ§Ζ÷≤ΦNΘ®0Θ§1Θ©Θ§Φ«Π’Θ®xΘ©=P(ΠΈ<x),‘ρœ¬Ν–Ϋα¬έ≤Μ’ΐ»ΖΒΡ « Θ® Θ©
AΘ°Π’Θ®0Θ©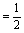
BΘ°Π’Θ®xΘ©=1-Π’(-x)
CΘ°P(|ΠΈ|<a)=2Π’(a)-1(a>0)
DΘ°P(|ΠΈ|>a)=1-Π’(a)(a>0)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΦΉΚΆ““Β»ΈεΟϊ÷Ψ‘Η’Ώ±ΜΥφΜζΒΊΖ÷ΒΫAΓΔBΓΔCΓΔ DΥΡΗω≤ΜΆ§ΒΡΗΎΈΜΖΰΈώΘ§ΟΩΗωΗΎΈΜ÷Ν…Ό”–“ΜΟϊ÷Ψ‘Η’ΏΘ§‘ρΦΉΚΆ““≤Μ‘ΎΆ§“ΜΗΎΈΜΖΰΈώΒΡΗ≈¬ ΈΣΘ® Θ©
DΥΡΗω≤ΜΆ§ΒΡΗΎΈΜΖΰΈώΘ§ΟΩΗωΗΎΈΜ÷Ν…Ό”–“ΜΟϊ÷Ψ‘Η’ΏΘ§‘ρΦΉΚΆ““≤Μ‘ΎΆ§“ΜΗΎΈΜΖΰΈώΒΡΗ≈¬ ΈΣΘ® Θ©
(A)  (B)
(B) 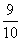 (C)
(C) 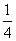
 (D)
(D) 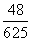
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
Ιέ≤λœ¬ΆΦΘΚ
1ΓΓ
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
Γ≠Γ≠
‘ρΒΎ____________––ΒΡΗς ΐ÷°ΚΆΒ»”Ύ2 0092.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com