
甲和乙等五名志愿者被随机地分到A、B、C、 D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )
D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )
(A) 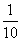 (B)
(B) 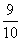 (C)
(C) 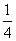
 (D)
(D) 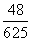
科目:高中数学 来源: 题型:
已知平面α⊥平面β,α∩β = l,点A∈α,A
= l,点A∈α,A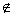 l,直线AB∥l,直线AC⊥l,直线m∥α
l,直线AB∥l,直线AC⊥l,直线m∥α ,m∥β,则下列四种位置关系中,不一定成立的是( )
,m∥β,则下列四种位置关系中,不一定成立的是( )
A. AB∥m B. AC⊥m C. AB∥β D. AC⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
四棱锥P-ABCD中,底面ABCD是一个平行四边形,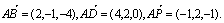
 (1)求证:PA⊥底面ABCD;
(1)求证:PA⊥底面ABCD;
(2)求四棱锥P-ABCD的体积;
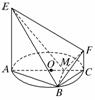
(3)对于向量a=(x1,y1,z1).b=(x2,y2,z2),c=(x3,y3,z3 )定义一种运算:
)定义一种运算:
(a×b)·c=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1试计算(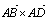 )
)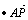 的绝对值的值;说明其与四棱锥P-ABCD体积的关系,并同此猜想这一运算(
的绝对值的值;说明其与四棱锥P-ABCD体积的关系,并同此猜想这一运算(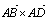 )
)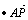 的绝对值的几何意义。
的绝对值的几何意义。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=6x-4(x=1,2,3,4,5,6)的值域为集合A,函数g(x)=2x-1(x=1,2,3,4,5,6)的值域为集合B,任意x∈A∪B,则x∈A∩B的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
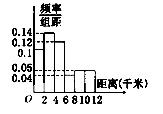
某公司为了改善职工的出行条件,随机抽取100名职工,调查了他们的居住地与公司间的距离(单位:千米).由其数据绘制的频率分布直方图如图所示,则样本中职工居住地与公司间的距离不超过4千米的人数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
用数学归纳法证明:“(n+1)·(n+2)·…·(n+n)=2n·1·3·…·(2n-1)”.从“k到k+1”左端需增乘的代数式为( )
A.2k+1 B.2(2k+1) C.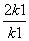 D.
D. 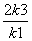
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数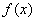 和
和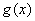 都是定义在集合
都是定义在集合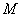 上的函数,对于任意的
上的函数,对于任意的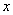
 ,都有
,都有
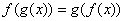 成立,称函数
成立,称函数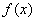 与
与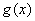 在
在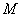 上互为“
上互为“ 函数”.
函数”.
(1)函数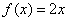 与
与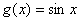 在
在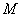 上互为“
上互为“ 函数”,求集合
函数”,求集合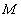 ;
;
(2)若函数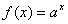 (
(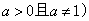 与
与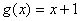 在集合
在集合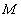 上互为 “
上互为 “ 函数”,
函数”,
求证: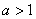 ;
;
(3)函数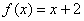 与
与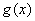 在集合
在集合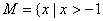 且
且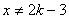 ,
,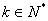
 上互为“
上互为“ 函数”,当
函数”,当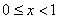 时,
时,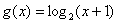 ,且
,且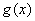 在
在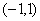 上是偶函数,求函数
上是偶函数,求函数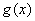 在集合
在集合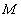 上的解析式.
上的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com