
设函数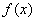 和
和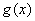 都是定义在集合
都是定义在集合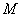 上的函数,对于任意的
上的函数,对于任意的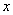
 ,都有
,都有
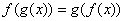 成立,称函数
成立,称函数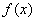 与
与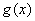 在
在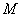 上互为“
上互为“ 函数”.
函数”.
(1)函数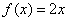 与
与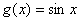 在
在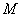 上互为“
上互为“ 函数”,求集合
函数”,求集合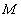 ;
;
(2)若函数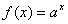 (
(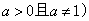 与
与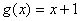 在集合
在集合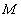 上互为 “
上互为 “ 函数”,
函数”,
求证: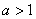 ;
;
(3)函数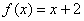 与
与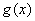 在集合
在集合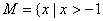 且
且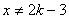 ,
,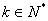
 上互为“
上互为“ 函数”,当
函数”,当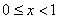 时,
时,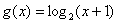 ,且
,且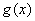 在
在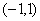 上是偶函数,求函数
上是偶函数,求函数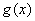 在集合
在集合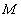 上的解析式.
上的解析式.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
甲和乙等五名志愿者被随机地分到A、B、C、 D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )
D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )
(A) 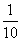 (B)
(B) 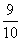 (C)
(C) 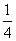
 (D)
(D) 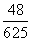
查看答案和解析>>
科目:高中数学 来源: 题型:
函数 ,其中
,其中 ,若动直线
,若动直线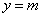 与函数
与函数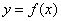 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为 ,则
,则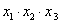 是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com