练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

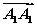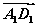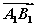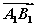    已知ABCD－A1B1C1D1为正方体，①(＋＋)2＝32；②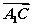·(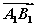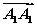－)＝0；③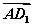向量与向量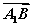的夹角是60°；④正方体ABCD－A1B1C1D1的体积为|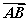··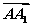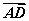|.其中正确命题的序号是________．


    ①     ②


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    曲线C：

       

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     如图，在正四棱锥S—ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总有PE⊥AC。

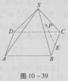
    （1）证明SB⊥AC；

    （2）指出动点P的轨迹，并证明你的结论；

    （3）以轨迹上的动点P为顶点的三棱锥P—CDE的最大体积为V1，正四棱锥S—ABCD的体积为V，则V1：V等于多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD，如图11-12。

         

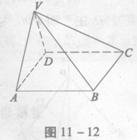
    （1）证明：AB⊥平面VAD；

    （2）求二面角A-VD-B的大小。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


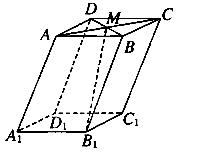
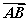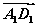    如图，在底面ABCD为平行四边形的四棱柱ABCD－A1B1C1D1中，M是AC与BD的交点，若＝a，＝b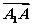，＝c则下列向量中与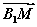相等的向量是(　　)

    A．－a＋b＋c           B.a＋b＋c

    C.a－b＋c                                 D．－a－b＋c

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    四棱锥P=ABCD中，AB⊥CD，CD⊥AD，PA⊥底面ABCD，PA=AD=CD=2AB=2，M为PC的中点。

    （1）求证BM∥平面PAD； 

    （2）在△PAD内找一点N，使MN⊥平面PBD；

    （3）求直线PC与平面PBD所成角的正弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某人有5把钥匙，其中有1把可以打开房门，但忘记了开门的是哪一把，于是他逐把不重复地试开，那么恰好第三次打开房门的概率是____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生．为了解学生的就业倾向，用分层抽样的方法从该校这四个专业共抽取40名学生进行调查，应在丙专业抽取的学生人数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝x3－12x在区间(k－1，k＋1)上不是单调函数，则实数k的取值范围是(　　)

    A．k≤－3或－1≤k≤1或k≥3          B．－3<k<－1或1<k<3

    C．－2<k<2                           D．不存在这样的实数

    查看答案和解析>>

    同步练习册答案