练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

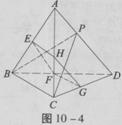
    如图10-4所示，在正三棱锥A—BCD中，∠BAC=30°，AB=a，平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于E、F、G、H。

    （1）判定四边形EFGH的形状，并说明理由；

    （2）设P是棱AD上的点，当AP为何值时，平面PBC⊥平面EFGH，请给出证明。


    （2）作CP⊥AD于P点，连接BP，∵AD⊥BC，∴AD⊥面BCP，∴HG∥AD，∴HG⊥面BCP，又HG面EFGH，∴面BCP⊥面EFGH，在Rt△APC中，∠CAP=30°，AC=a, ∴AP=.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若则  （  ）

    A．-1     B．1           C．-     D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    圆心在直线2x-y-7=0上的圆C与y轴交于两点A(0,-4),B(0,-2),则圆C的方程为_____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    经过点作圆的弦，使得点平分弦，则弦所在直线的方程为               ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图10-8，在三棱锥S—ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2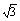，M、N分别为AB、SB的中点。

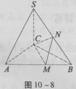    （1）证明：AC⊥SB；

    （2）求二面角N—CM—B的大小；

     （3）求点B到平面CMN的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知平面α⊥平面β，α∩β= l，点A∈α，A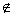l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（    ）

    A. AB∥m        B. AC⊥m    C. AB∥β   D. AC⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    菱形ABCD的边AB=5，对角线BD=6，沿BD折叠得四面体ABCD，已知该四面体积不小于8，求二面角A—BC—C的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正方体ABCD-A1B1C1D1中，M、N分别是棱AA1和BB1的中点，则CM与D1N夹角的正弦值为  （  ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某公司为了改善职工的出行条件，随机抽取100名职工，调查了他们的居住地与公司间的距离(单位：千米)．由其数据绘制的频率分布直方图如图所示，则样本中职工居住地与公司间的距离不超过4千米的人数为________．

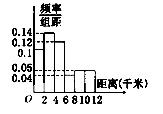
    查看答案和解析>>

    同步练习册答案