
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
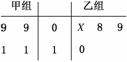
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名 同学,求这两名同学的植树总棵数为19的概率.
同学,求这两名同学的植树总棵数为19的概率.
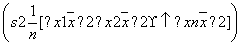
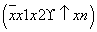
 (2)记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,11;乙组四名同学为B1
(2)记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,11;乙组四名同学为B1 ,B2,B3,B4,他们植树的棵数依次为9,8,9,10.分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,它们是:
,B2,B3,B4,他们植树的棵数依次为9,8,9,10.分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,它们是:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A3,B2),(A3,B3),(A3,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结果有4个,它们是:(A1,B4),(A2,B4),(A3,B2),(A4,B2),
故所求概率为P(C)=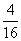 =
=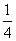 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
如图,直四棱柱ABCD—A1B1C1D1的底面ABCD为平行四边形,其中AB=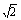 ,BD=BC=1,AA1=2,E为DC中点,点F在DD1上,且DF=
,BD=BC=1,AA1=2,E为DC中点,点F在DD1上,且DF=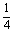 。
。
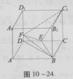
(1)求异面直线BD与A1D1的距离;
(2)EF与BC1是否垂直?请说明理由;
(3)求二面角E—FB—D的正切值。
查看答案和解析>>
科目:高中数学 来源: 题型:
四棱锥P=ABCD中,AB⊥CD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
(1)求证BM∥平面PAD;
(2)在△PAD内找一点N,使MN⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
从某社区家庭中按分层抽样的方法,抽取100户高、中、低收入家庭调查社会购买力的某项指标,若抽出的家庭中有56户中等收入户和19户低收入户,已知该社区高收入家庭有125户,则该社区家庭总户数为__________
查看答案和解析>>
科目:高中数学 来源: 题型:
某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生.为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com